Проектирование механизма по заданным условиям
Рис. 4 Положение направляющей поступательной пары D характеризуется коэффициентом Kv изменения средней скорости ползуна. Крайние положения ползуна 5, определяющие его ход H, соответствуют точкам пересечения A’ и A” направляющей ползуна с траекторией точки A кривошипа 1.При вращение кривошипа камень 2 скользит по кулисе 3, при этом параметры механизма ( Кривошипа из положения ОА’ в положение OA”.Реверсное перемещение D’D” (прямой ход ползуна) соответствует дальнейшему повороту кривошипа на угол Центр вращения Е кулисы 3 лежит на пересечении направляющей поступательной пары и биссектрисы угла A’OA”. Поэтому длина кривошипа Из соотношения
Полученные результаты:
l1=0,176 м; l3=0,221 м; l4=0,375 м;
Теперь установим зависимости координат всех точек механизма от угла поворота кривошипа. Для этого воспользуемся пакетом MathCad. Зададим вспомогательный угол, соответствующий крайнему положению ползуна.
Выразим координаты точки A механизма:
Через вспомогательные углы геометрии найдем координаты точек С, D и центра масс S3, S4:
Координаты точки С.
Координаты точкиD.
Координаты центров масс звена 4.
Так как Координаты центров масс звена 3
Таким образом, все зависимости в механизме нам известны. Можно приступать к исследованию закона его движения.
|

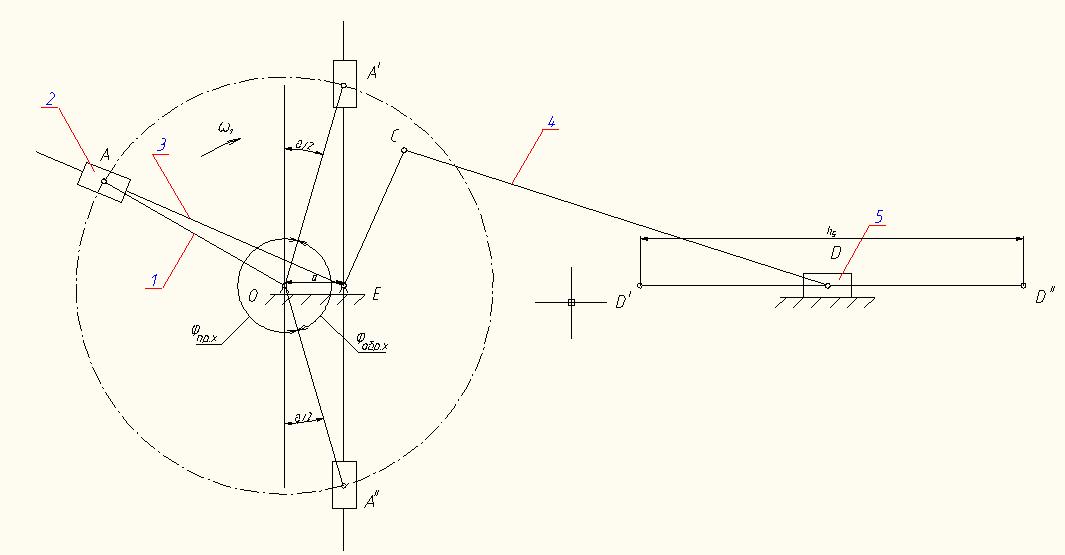
 и а) выбраны так, что кулиса совершает непрерывное вращательное движение. Перемещение ползуна из положения D” в положение D’(обратный ход) соответствует равномерному вращению (угол
и а) выбраны так, что кулиса совершает непрерывное вращательное движение. Перемещение ползуна из положения D” в положение D’(обратный ход) соответствует равномерному вращению (угол  )
) . Эти углы не равны, и различаются на угол перекрытия
. Эти углы не равны, и различаются на угол перекрытия  .
.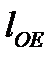 между осями вращения кривошипа и кулисы связаны следующим соотношением:
между осями вращения кривошипа и кулисы связаны следующим соотношением: 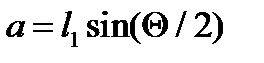 . Зная одну из этих величин, всегда можно найти другую. Длина кривошипа
. Зная одну из этих величин, всегда можно найти другую. Длина кривошипа  дополнительной группы CD равна половине хода ползуна,
дополнительной группы CD равна половине хода ползуна,  .
. которое равняется 1/3 получаем, что
которое равняется 1/3 получаем, что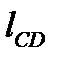 =0,375 (м)
=0,375 (м) , так как
, так как 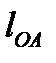 =0,176 (м)
=0,176 (м)


















