Уравнивание нивелирных полигонов
Ходы технического нивелирования разделяются на две основные группы: свободные системы и несвободные системы. Свободные системы характеризуются наличием в каждой из них лишь одного пункта с твердой отметкой. Несвободные системы опираются на два и большее число твердых пунктов. Свободные системы прокладываются в виде одиночного замкнутого полигона или в виде систем замкнутых полигонов. Иногда прокладываются висячие ходы, опирающиеся на один пункт с известной отметкой. В этих случаях нивелирование по ходу выполняется в прямом и обратном направлениях или двумя нивелирами в одном направлении. Несвободные системы представляют собой одиночные ходы, опирающиеся на концах на два пункта с твердыми отметками, или образуют системы ходов с одной или несколькими узловыми точками, опирающиеся на твердые пункты. При уравнивании несвободной сети вводятся фиктивные звенья, соединяющие исходные реперы (пунктиром). Фиктивные звенья намечают так, чтобы они не пересекали действительные и чтобы дополнительные полигоны имели наименьшее число действительных звеньев. В результате получаются дополнительные полигоны. При вычислениях системы замкнутых свободных полигонов технического нивелирования наиболее рациональным является применение способа полигонов проф. В.В. Попова. Сущность уравнивания сводится к последовательному распределению невязок в полигонах пропорционально красным числам. Быстрота сходимости приближений в методе полигонов зависит от знаков невязок и их величины в смежных полигонах. Уравнивание системы замкнутых свободных полигонов рассмотрим на примере. Система из шести ходов технического нивелирования с четырьмя узловыми точками (в числе которых одна – стенная марка 1 – является твердой) образует три замкнутых полигона. Каждый полигон в сети граничит не менее, чем с двумя другими полигонами. Составляется схема ходов (рисунок 37), на которой приводятся все данные, необходимые для уравнивания: суммарные превышения по звеньям, hм; длина звеньев Lкм и отметка исходной марки Нстен. марки 1 = 52,130 м.
Как в свободных, так и в несвободных системах количество полигонов определяется по формуле: r = N + T – 1(241) где N – число сомкнутых полигонов; Т – число исходных реперов. В нашем примере r = 3 + 1 – 1 = 3 Уравнивание выполняется в следующей последовательности. 1. Подсчитывают фактические невязки в превышениях по каждому полигону, соответствующие обходу полигона по ходу часовой стрелки, по формулам: в замкнутых полигонах fh = åh (242) в разомкнутых fh = åh – (Нк – Нн) (243) и суммарные длины звеньев (периметр полигона) åL. Подсчитывают допустимые невязки по формулам: для технического нивелирования fh доп = ± 50 мм Ö Lкм (244) для нивелирования IV класса fh доп = ± 20 мм Ö Lкм (245) Результаты этих вычислений записывают на том же чертеже. Римскими цифрами нумеруют полигоны вначале сомкнутые, а потом разомкнутые. 2. Убедившись в допустимости невязок, переходят к уравниванию сети. Для этого строят рабочий чертеж сети более крупных размеров, на котором и производят уравнивание (рисунок 38).
Рисунок 38 Рабочая схема
3. На рабочем чертеже в центре каждого полигона строят двойные рамочки, над которыми римскими цифрами пишут номера полигонов, а внутри – вычисленные невязки fh в мм. Затем вне каждого полигона у каждого звена строят рамочки для записи поправок. Таким образом, у внешних звеньев будет по одной, а у внутренних – по две рамочки (по одной с каждой стороны звена). На фиктивные звенья рамочки не строят. 4. Для каждого звена вычисляют красные числа
Красное число – это отношение длины звена к периметру полигона. Контроль: Сумма красных чисел для полигона должна равняться единице. Красные числа подписывают над соответствующими рамочками, расположенными вне полигона около его звеньев красным цветом. Так в полигоне I красные числа равны 6,3: 12,6 = 0,50; 3,4: 12,6 = 0,27; 2,9: 12,6 = 0,23 Контроль вычислений: 0,50 + 0,27 + 0,23 = 1.0 5. Распределение невязок начинают с I полигона. Умножив невязку (+21) на его красные числа, полученные результаты, сумма которых должна быть равна распределяемой невязке, записывают в соответствующих данному полигону табличках. Распределенную невязку подчеркивают. В I полигоне +21 ´ 0,50 = +10 +21 ´ 0,27 = + 6; 21 ´ 0,23 = + 5 Контроль вычислений: +10 +6 +5 = 21 6. Находят значение невязки во II полигоне, учитывая поправку из первого полигона (- 18 + 6 = -12). Учтенную невязку подчеркивают. Новую невязку распределяют пропорционально красным числам II полигона (0,46; 0,33; 0,21) и полученные результаты (- 5; - 4; - 3), сумма которых должна быть равна невязке, записывают во внешних к полигону табличках под соответствующими красными числами. Распределенную невязку подчеркивают. 7. Находят новую невязку III полигона, учитывая поправки из I и II полигонов (- 17 – 3 -+ 5 = - 15). Учтенные поправки подчеркивают. Откорректированную невязку - 15 распределяют таким же путем, как и в первых двух полигонах и подчеркивают. 8. Далее переходят ко второму кругу распределения невязок. Здесь появилась новая невязка, равная сумме поправок, перешедших из смежных полигонов. Эта невязка распределяется так же, как и первый раз. Закончив первый цикл распределения невязок, приступают ко второму, затем к третьему и так далее до тех пор, пока все невязки полигонов станут равными нулю. Следует помнить, что во избежание повторного использования одной и той же величины в процессе распределения невязок, каждое использованное значение необходимо сразу же подчеркнуть. 9. Находят окончательное значение поправок. Подсчитывают алгебраическую сумму поправок в каждой табличке. Для внешних ходов эти суммы, взятые с обратным знаком, будут окончательными поправками. Их выписывают в скобках внутри полигонов: в первом полигоне -8, во втором + 8, в третьем + 9. Для каждого общего хода двух смежных полигонов имеются по две таблички, расположение по разные стороны хода. Внешние суммы полигона переносят внутрь полигона с противоположным знаком и складывают с его внутренними суммами для тех же звеньев. Полученные поправки записывают в скобках около соответствующих звеньев. Около внутренних звеньев сети поправки записывают по обе стороны звена. 10. В каждом полигоне сумма поправок на звенья должна быть равна невязке полигона с обратным знаком, например I полигон - 3 – 10 – 8 = - 21 = - (+ 21) II полигон +10 + 8 + 0 = + 18 = - (- 18) III полигон 0 + 9 + 8 = + 17 = - (- 17). 11. Введя поправки в измеренные превышения, получают исправленные их значения, по которым вычисляют отметки узловых точек (таблица 7).
Таблица 7 – Вычисление отметок узловых точек
12. Производится оценка точности. Средняя квадратическая погрешность превышения на 1 км нивелирного хода m вычисляется (таблица 8) по формуле
где Рi = Таблица 8 Определение средней квадратической погрешности превышения на 1 км нивелирного хода
Средняя квадратическая погрешность превышения на 1 км нивелирного хода равна
|

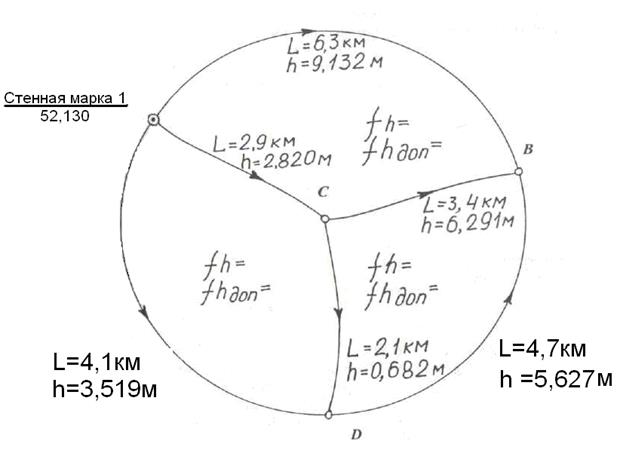 Рисунок 37 Схема свободной сети нивелирных полигонов
Рисунок 37 Схема свободной сети нивелирных полигонов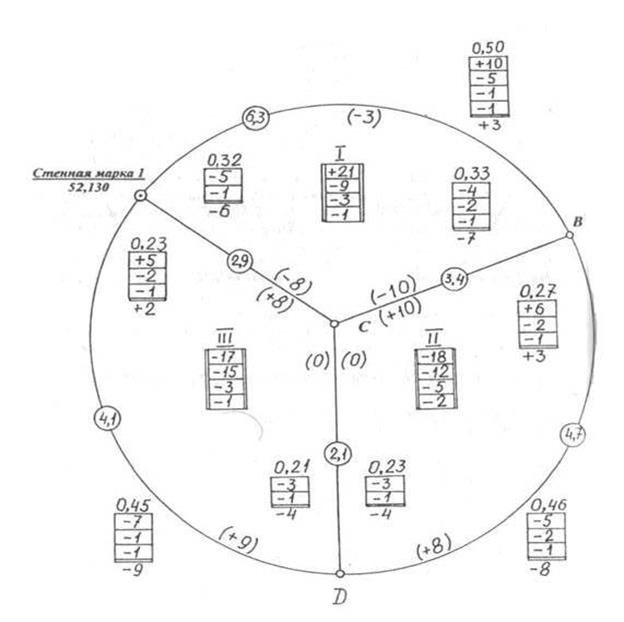
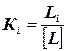 (246)
(246)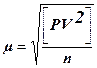 (247)
(247) ; L – длина звеньев в км; n – число полигонов
; L – длина звеньев в км; n – число полигонов
 мм.
мм.


