Интегрирование неправильных рациональных дробей
Всякую неправильную рациональную дробь
а) если дробь неправильная, то ее нужно представить в виде суммы многочлена и правильной дроби; б) разложить знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей; в) проинтегрировать многочлен и полученную сумму простейших дробей. Рассмотрим примеры. 2.6.5 Корни знаменателя действительные и различные Пример 22. Найти интеграл Решение. Дробь под знаком интеграла правильная, так как степень числителя меньше степени многочлена. а) Разложим знаменатель на простые множители
Найдем корни квадратного трехчлена по теореме Виета:
Тогда б) Подынтегральную функцию представим в виде суммы простейших дробей с неопределенными коэффициентами
Правую часть приведем к общему знаменателю
Так как две дроби равны и равны их знаменатели, то будут тождественно равны и числители
Для нахождения неопределенных коэффициентов применим метод отдельных значений аргумента: аргументу
Пусть
отсюда
Пусть
отсюда
в) Таким образом, интеграл может быть представлен в виде суммы трех простейших интегралов
2.6.6 Корни знаменателя действительные, среди них есть кратные Пример 23. Найти интеграл Решение. а) Разложим знаменатель на простые множители. Методом подбора можно установить, что один корень равен 1, тогда многочлен
Имеем
б) Подынтегральная функция может быть представлена в виде суммы простейших дробей с неопределенными коэффициентами
Правую часть приведем к общему знаменателю, получим
Приравняем числители, получим тождество
Пусть
Пусть
Так как действительных корней больше нет, то примем для
В данное равенство подставим известные значения в) Таким образом,
2.6.7 Корни знаменателя комплексные и различные Пример 24. Найти интеграл Решение. Под знаком интеграла правильная рациональная дробь, так как степень многочлена числителя меньше степени многочлена знаменателя. Квадратный трехчлен
Приведем правую часть к общему знаменателю, получим равенство двух дробей
Данные дроби равны, если тождественно равны их числители
Раскроем в правой части скобки и сгруппируем слагаемые с одинаковыми степенями:
Два многочлена тождественно равны, когда равны коэффициенты при одинаковых степенях
Решим систему методом Гаусса, для этого выпишем расширенную матрицу из коэффициентов при неизвестных и свободных членов и сведем ее к ступенчатому виду:
Первую строку умножим на
Третью строку умножим на 8 и сложим с четвертой строкой, получим матрицу
Четвертую строку разделим на 17, получим матрицу
Запишем систему уравнений для полученной матрицы:
Таким образом, интеграл может быть представлен в виде суммы двух интегралов:
2.6.8 Среди комплексных корней знаменателя есть кратные Пример 25. Найти интеграл Решение. Дробь, стоящая под знаком интеграла правильная, так как степень многочлена в числителе меньше степени многочлена в знаменателе. Знаменатель дроби имеет комплексные корни, причем среди них есть кратные. Поэтому подынтегральная функция может быть представлена в виде суммы трех простейших дробей:
Приводя правую часть к общему знаменателю, получим равенство двух дробей
Приравняем числители дробей, получим тождество:
Раскроем скобки и приведем подобные:
Приравняем коэффициенты при одинаковых степенях
Решим систему уравнений методом Гаусса:
Первую строку матрицы умножим на (-5) и сложим с третьей строкой, вторую строку умножим на (-5) и сложим с четвертой строкой, первую строку умножим на (-4) и сложим с пятой строкой, вторую строку умножим на (-4) и сложим с шестой строкой, получим следующую матрицу:
Третью строку матрицы умножим на (-4) и сложим с пятой строкой, четвертую строку умножим на (-4) и сложим с шестой строкой, получим матрицу:
Запишем систему уравнений, соответствующую данной матрице:
Таким образом, интеграл можно представить в виде суммы трех интегралов:
2.6.9 Общий случай Пример 26. Найти интеграл Решение. а) Рациональная дробь, стоящая под знаком интеграла, неправильная, так как степень многочлена в числителе больше степени многочлена в знаменателе. Выделим ее целую часть путем деления числителя на знаменатель:
Дробь можно представить в виде суммы целой части и правильной рациональной дроби:
б) Разложим правильную рациональную дробь на сумму простейших дробей:
Квадратный трехчлен в) Правую часть приведем к общему знаменателю, тогда получим
Данные дроби будут равны, если тождественно равны их числители:
Преобразуем:
Приравниваем коэффициенты при одинаковых степенях
Итак, имеем
г) Интегрируем полученное равенство:
Любая рациональная функция интегрируется в элементарных функциях.
|

 можно путем деления числителя на знаменатель представить в виде суммы многочлена
можно путем деления числителя на знаменатель представить в виде суммы многочлена  и правильной рациональной дроби
и правильной рациональной дроби 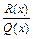 , то есть
, то есть .
. .
. .
.
 .
. .
. .
. . (6)
. (6) придают конкретные значения столько раз, сколько неопределенных коэффициентов. Обычно берут за
придают конкретные значения столько раз, сколько неопределенных коэффициентов. Обычно берут за  . Подставим это значение в левую и правую части тождества (6), получим
. Подставим это значение в левую и правую части тождества (6), получим .
. .
.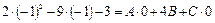 ,
, .
. .
. ,
, .
.
 .
. .
. делится без остатка на
делится без остатка на 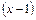 . Разделим
. Разделим
 .
.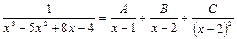 .
. .
. .
.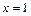 , тогда
, тогда ,
,  .
. , тогда
, тогда ,
,  .
. , тогда
, тогда .
. и
и  , найдем
, найдем  :
:  ,
,  ,
, 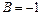 .
.
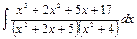 .
. не имеет действительных корней, так как дискриминант
не имеет действительных корней, так как дискриминант  . Оба множителя знаменателя не имеют действительных корней, то есть корни знаменателя комплексные, поэтому подынтегральная функция может быть представлена в виде суммы двух простейших дробей
. Оба множителя знаменателя не имеют действительных корней, то есть корни знаменателя комплексные, поэтому подынтегральная функция может быть представлена в виде суммы двух простейших дробей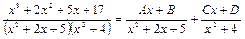 .
. .
. .
.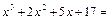
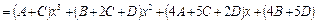 .
.
 .
. и сложим с третьей строкой, вторую строку умножим на
и сложим с третьей строкой, вторую строку умножим на  .
. .
. .
.

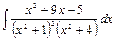 .
. .
.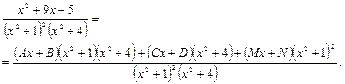



 , получим систему уравнений:
, получим систему уравнений:
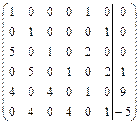 .
.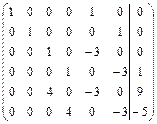 .
. .
.


 Четвертый интеграл возьмем по рекуррентной формуле (1)
Четвертый интеграл возьмем по рекуррентной формуле (1) 

 .
.
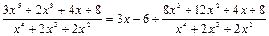 .
.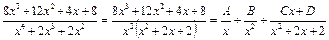 .
. не имеет действительных корней.
не имеет действительных корней. .
. .
.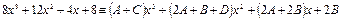 .
.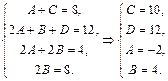
 .
.



