Понятие неопределенного интеграла. В дифференциальном исчислении решается задача: по данной функции найти ее производную
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
В дифференциальном исчислении решается задача: по данной функции Определение 1. Функция
Например, первообразной функции Очевидно, что Теорема 1. Если функция Определение 2. Множество всех первообразных функций Таким образом, по определению
Здесь
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции. Геометрически неопределенный интеграл представляет собой семейство параллельных кривых
Всякая непрерывная на Результат интегрирования проверяется дифференцированием.
|
найти ее производную. Интегральное исчисление решает обратную задачу: найти функцию 
, зная ее производную.
называется первообразной функции 
, если для любого 
выполняется равенство
.
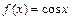является функция 
, так как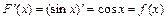 
.
, где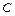 
– постоянное слагаемое, также является первообразной функции 
.
, где 
.
.
– подынтегральное выражение,
– переменная интегрирования,
– знак неопределенного интеграла.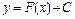
. График первообразной называется интегральной кривой (см. рисунок 1).
