Интегрирование иррациональных функций
2.8.1 Интеграл вида Подынтегральная функция с помощью подстановки Пример 36. Найти интеграл Решение. Сделаем подстановку
Под знаком интеграла – неправильная рациональная дробь. Путем деления числителя на знаменатель выделим целую часть и представим дробь в виде суммы целой части и правильной рациональной дроби:
Итак, Тогда
2.8.2 Интеграл вида Данный интеграл сводится к интегралу от рациональной функции с помощью подстановки Пример 37. Найти интеграл Решение. Сделаем подстановку
Найдем
Подставим в интеграл и получим
2.8.3 Интегралы вида а) б) в) г) В данных интегралах используют тригонометрические подстановки. а)
Пример 38. Найти интеграл Решение. Сделаем подстановку
б)
Пример 39. Найти интеграл Решение. Сделаем подстановку
в)
Пример 40. Найти интеграл Решение. Сделаем подстановку
г) Пример 41. Найти интеграл Решение. Выделим полный квадрат в подкоренном выражении:
Сделаем подстановку
2.8.4 Интегралы вида В данных интегралах делается подстановка Пример 42. Найти интеграл Решение. Пусть
2.8.5 Интегралы вида Данный интеграл можно найти, пользуясь формулой:
где Для нахождения неопределенных коэффициентов дифференцируют обе части равенства (10), получают
Умножают обе части данного равенства на
Далее следует приравнять коэффициенты при одинаковых степенях Пример 43. Найти интеграл Решение. Пусть
Продифференцируем левую и правую части данного равенства
Используем свойства интеграла и правила дифференцирования, получим
Умножим обе части равенства на
преобразуем
Приравниваем коэффициенты при одинаковых степенях
Найденные коэффициенты подставим в равенство (11), тогда
2.8.6 Интегрирование дифференциального бинома Для нахождения данного интеграла используют подстановки Чебышева П.А.: а) если б) если в) если В других случаях интегралы данного вида не выражаются через элементарные функции. Пример 44. Найти интеграл Решение. В данном интеграле Подстановка
Тогда
2.9 Интегралы, «неберущиеся» через элементарные функции Всякая непрерывная функция имеет первообразную. Если первообразная является элементарной функцией, то говорят, что
Эти интегралы имеют большое значение в приложениях, для них составлены таблицы значений для различных значений аргумента
|

 , где
, где  – рациональная функция
– рациональная функция ,
,  , где
, где  – наименьший общий знаменатель дробей
– наименьший общий знаменатель дробей  преобразуется в рациональную функцию от
преобразуется в рациональную функцию от  .
. .
. , где 6 – наименьший общий знаменатель дробей
, где 6 – наименьший общий знаменатель дробей  ,
,  ; найдем
; найдем 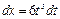 . Тогда
. Тогда .
.
 .
.



 , где
, где  и найти
и найти 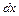 .
.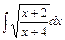 .
. . Выразим из данного равенства
. Выразим из данного равенства  ,
,  ,
, ,
,  .
.
 К данному интегралу применяем метод интегрирования по частям:
К данному интегралу применяем метод интегрирования по частям:  , тогда
, тогда 

 Вернемся к старой переменной
Вернемся к старой переменной 



 ,
, ,
, ,
, .
. ,
,  ,
, 
 .
. .
. ,
,  ,
,  , получим
, получим




 ,
, ,
,  ,
,  ,
,  .
. .
. ,
,  ,
,  ,
,  . Тогда
. Тогда


 .
. ,
, ,
,  ,
,  ,
,  .
. .
. ,
,  ,
,  ,
,  , получим
, получим






 . В результате выделения полного квадрата в подкоренном выражении, приходим к одному из интегралов вида а)-в) в данном пункте.
. В результате выделения полного квадрата в подкоренном выражении, приходим к одному из интегралов вида а)-в) в данном пункте. .
.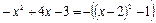 .
. , тогда
, тогда  ,
,  , тогда:
, тогда:
 Для нахождения первого интеграла используем метод подведения под знак дифференциала:
Для нахождения первого интеграла используем метод подведения под знак дифференциала:  , тогда
, тогда  . Для нахождения второго интеграла используем тригонометрическую подстановку:
. Для нахождения второго интеграла используем тригонометрическую подстановку:  ,
,  ,
, 



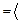 Вернемся к старой переменной:
Вернемся к старой переменной:  , тогда
, тогда 




 , отсюда
, отсюда  ,
,  .
. .
. ,
,  ,
, 

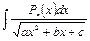 , где
, где  – многочлен степени
– многочлен степени 
 , (10)
, (10)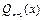 – многочлен степени
– многочлен степени  с неопределенными коэффициентами,
с неопределенными коэффициентами,  – также неопределенный коэффициент.
– также неопределенный коэффициент.
 .
. , получают
, получают .
. . Таким образом, находят многочлен
. Таким образом, находят многочлен  .
. . (11)
. (11)


 ,
, .
.


 , где
, где  ,
,  – действительные числа,
– действительные числа,  ,
,  – рациональные числа
– рациональные числа , где
, где  – наименьший общий знаменатель дробей
– наименьший общий знаменатель дробей  – целое число, то вводят подстановку
– целое число, то вводят подстановку  , где
, где  – целое число, то используют подстановку
– целое число, то используют подстановку  , где
, где  .
. ,
,  ,
,  ,
,  – целое число, следовательно, имеем случай б).
– целое число, следовательно, имеем случай б). . Отсюда
. Отсюда  ,
, .
.


 выражается через элементарные функции. Если интеграл не выражается через элементарные функции, то говорят, что он «не берется». К таковым относятся следующие интегралы:
выражается через элементарные функции. Если интеграл не выражается через элементарные функции, то говорят, что он «не берется». К таковым относятся следующие интегралы: – интеграл Пуассона (теория вероятностей),
– интеграл Пуассона (теория вероятностей), ,
,  – интегралы Френеля (физика),
– интегралы Френеля (физика), – интеграл логарифма (теория чисел),
– интеграл логарифма (теория чисел), ,
,  – интегральные синус и косинус,
– интегральные синус и косинус, – интегральная показательная функция.
– интегральная показательная функция.


