Интегрирование по частям. Если функции и имеют непрерывные производные на отрезке , то имеет место формула
Если функции
Пример 47. Вычислить интеграл Решение.
Интегрирование четных и нечетных функций в симметричных пределах Пусть функция Докажем, что, если функция
Разобьем отрезок
Применим к первому интегралу подстановку
Используя свойство определенного интеграла
и подставим в равенство (13), получим
Пусть функция Запишем интеграл в виде суммы двух интегралов
К первому интегралу применим подстановку
подставляем в равенство (12):
Несобственные интегралы Определенные интегралы от непрерывной функции, но с бесконечным промежутком интегрирования или определенные интегралы с конечным промежутком интегрирования, но от неограниченной функции, называются несобственными интегралами.
|
и 
имеют непрерывные производные на отрезке 
, то имеет место формула
.
.
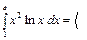Применим метод интегрирования по частям: 
, тогда 
непрерывна на отрезке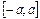 
, симметричном относительно точки 
.
, то
.
и 
. Тогда по свойству аддитивности интеграла запишем
(13)
, тогда 
, если 
и если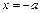 
, то 
. Тогда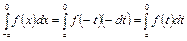
.
, перепишем интеграл в виде:
поскольку определенный интеграл не зависит от обозначения переменной интегрирования, то 
.
.
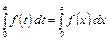
– для четной функции.
,
.
