Определение 3. Функция вида
 ,
,
где  натуральное число,
натуральное число,  – постоянные коэффициенты, называется многочленом или целой рациональной функцией. Число
– постоянные коэффициенты, называется многочленом или целой рациональной функцией. Число  – степень многочлена.
– степень многочлена.
Определение 4. Корнем многочлена 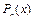 называется такое значение
называется такое значение 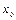 , при котором многочлен обращается в нуль, то есть
, при котором многочлен обращается в нуль, то есть  .
.
Теорема 2. Если  – корень многочлена
– корень многочлена 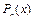 , то многочлен делится без остатка на
, то многочлен делится без остатка на  , то есть
, то есть
 ,
,
где  – многочлен степени
– многочлен степени  .
.
Теорема 3 (основная теорема алгебры). Всякий многочлен  -й степени имеет, по крайней мере, один корень, действительный или комплексный.
-й степени имеет, по крайней мере, один корень, действительный или комплексный.
Теорема 4. Всякий многочлен 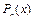 можно представить в виде
можно представить в виде
 ,
,
где  ,
,  , …,
, …,  – корни многочлена,
– корни многочлена,  – коэффициент многочлена при
– коэффициент многочлена при  .
.
Теорема 5. Два многочлена тождественно равны друг другу тогда и только тогда, когда коэффициенты одного многочлена равны соответствующим коэффициентам другого.
Теорема 6. Если многочлен 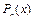 с действительными коэффициентами имеет комплексный корень
с действительными коэффициентами имеет комплексный корень  , то он имеет и сопряженный корень
, то он имеет и сопряженный корень  .
.
Теорема 7. Всякий многочлен с действительными коэффициентами разлагается на линейные и квадратные множители, дискриминант которых меньше нуля, с действительными коэффициентами, то есть

При этом  . Все квадратные трехчлены не имеют действительных корней. Например, разложим на множители многочлены
. Все квадратные трехчлены не имеют действительных корней. Например, разложим на множители многочлены
 ;
;
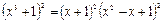 ;
;
 .
.

 ,
, натуральное число,
натуральное число,  – постоянные коэффициенты, называется многочленом или целой рациональной функцией. Число
– постоянные коэффициенты, называется многочленом или целой рациональной функцией. Число 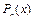 называется такое значение
называется такое значение 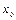 , при котором многочлен обращается в нуль, то есть
, при котором многочлен обращается в нуль, то есть  .
. – корень многочлена
– корень многочлена  , то есть
, то есть ,
, – многочлен степени
– многочлен степени  .
. ,
, , …,
, …,  – корни многочлена,
– корни многочлена,  – коэффициент многочлена при
– коэффициент многочлена при  .
. , то он имеет и сопряженный корень
, то он имеет и сопряженный корень  .
.
 . Все квадратные трехчлены не имеют действительных корней. Например, разложим на множители многочлены
. Все квадратные трехчлены не имеют действительных корней. Например, разложим на множители многочлены ;
;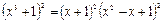 ;
; .
.


