Метод непосредственного интегрирования
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции приводится к табличному интегралу, называется непосредственным интегрированием. Пример 4. Найти интеграл Решение.
Сделаем проверку, для чего найдем производную от функции
Получили подынтегральную функцию, следовательно, интеграл нашли правильно. Пример 5. Найти интеграл Решение.
Метод подведения под знак дифференциала Если подынтегральное выражение содержит некоторую функцию и ее производную, то в этом случае используют метод подведения под знак дифференциала:
При сведении интеграла к табличному используют следующие преобразования:
Например, Пример 6. Найти интеграл Решение. Заметим, что дифференциал от функции, стоящей под знаком корня, имеет вид
Пример 7. Найти интеграл Решение. Заметим, что в подынтегральном выражении есть функция
|
.
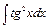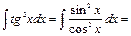
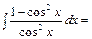
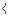числитель почленно разделим на знаменатель и запишем данный интеграл в виде разности двух интегралов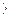 
.
.
.
.
.
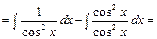
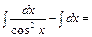
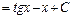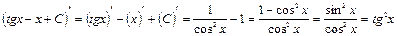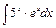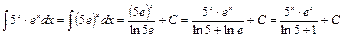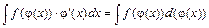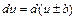, b – число,
,
,
.
.
.
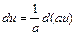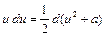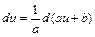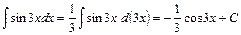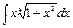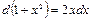. В подынтегральном выражении есть 
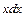, то есть это 
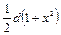. Тогда получим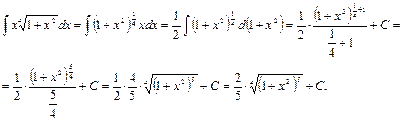
.
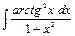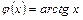и ее производная 
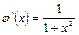. Тогда выражение 
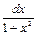является дифференциалом функции 
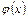, то есть 
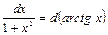. Используя метод подведения под знак дифференциала, найдем интеграл
.
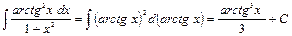