I)  ; (2)
; (2)
II) 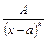 ; (3)
; (3)
III)  ; (4)
; (4)
IV) 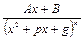 . (5)
. (5)
Определение 6. Дроби вида I-IV называются простейшими рациональными дробями. Квадратный трехчлен 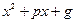 не имеет действительных корней.
не имеет действительных корней.
Интегрирование простейших дробей вида I-IV не составляет большой трудности.
I). 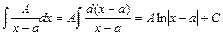 .
.
II). 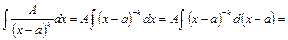
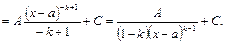
III). 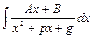 . В числителе выделим производную квадратного трехчлена и преобразуем числитель:
. В числителе выделим производную квадратного трехчлена и преобразуем числитель:
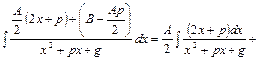
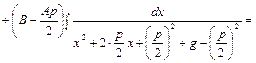
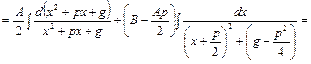
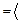
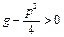 , так как квадратный трехчлен не имеет действительных корней
, так как квадратный трехчлен не имеет действительных корней 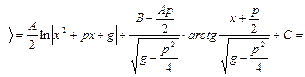
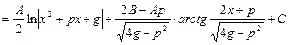 .
.
IV). 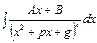
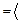 В числителе выделим производную квадратного трехчлена
В числителе выделим производную квадратного трехчлена  , тогда
, тогда 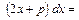
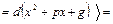
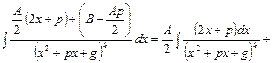
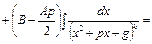
 Во втором интеграле выделим полный квадрат в знаменателе
Во втором интеграле выделим полный квадрат в знаменателе 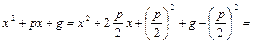
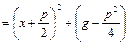 . Введем новую переменную
. Введем новую переменную 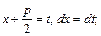
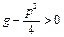 , обозначим
, обозначим 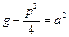
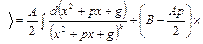
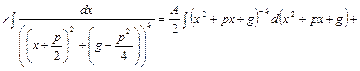
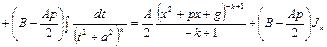 .
.
Интеграл  берем по рекуррентной формуле (1).
берем по рекуррентной формуле (1).
Пример 19. Найти интеграл 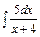 .
.
Решение.
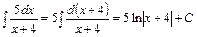 .
.
Пример 20. Найти интеграл 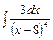 .
.
Решение.
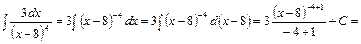

Пример 21. Найти интеграл 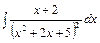 .
.
Решение.
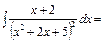
 В числителе выделим производную квадратного трехчлена
В числителе выделим производную квадратного трехчлена 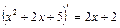 , тогда
, тогда 
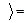
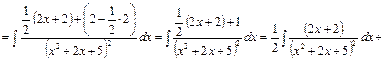
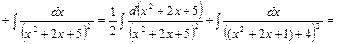
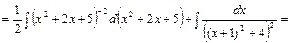

 ко второму интегралу применим рекуррентную формулу
ко второму интегралу применим рекуррентную формулу 
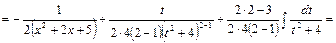
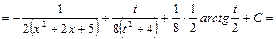
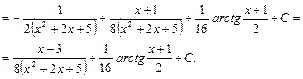
Теорема 8. Всякую правильную рациональную дробь  , знаменатель которой разложен на множители
, знаменатель которой разложен на множители
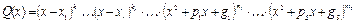 ,
,
можно представить и притом единственным образом в виде суммы простейших дробей:
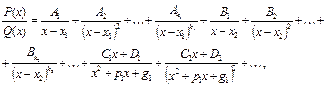
где 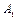 ,
, 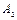 , …,
, …,  ,
,  , …,
, …,  ,
,  , …,
, …, 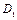 ,
, 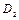 , … – некоторые действительные коэффициенты.
, … – некоторые действительные коэффициенты.
1) Линейным множителям  будут соответствовать простейшие дроби I-II видов.
будут соответствовать простейшие дроби I-II видов.
2) Квадратным множителям  будут соответствовать простейшие дроби III-IV видов.
будут соответствовать простейшие дроби III-IV видов.
3) Число простейших дробей, соответствующих линейному или квадратному множителю  , равно степени, в которой этот множитель входит в разложение
, равно степени, в которой этот множитель входит в разложение  .
.

 ; (2)
; (2)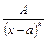 ; (3)
; (3) ; (4)
; (4)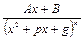 . (5)
. (5)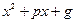 не имеет действительных корней.
не имеет действительных корней.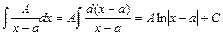 .
.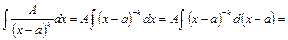
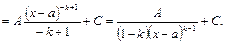
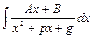 . В числителе выделим производную квадратного трехчлена и преобразуем числитель:
. В числителе выделим производную квадратного трехчлена и преобразуем числитель: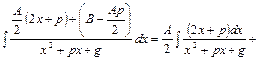
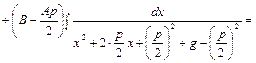
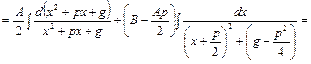
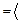
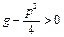 , так как квадратный трехчлен не имеет действительных корней
, так как квадратный трехчлен не имеет действительных корней 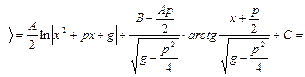
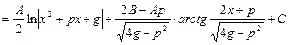 .
.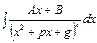
 , тогда
, тогда 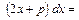
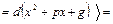
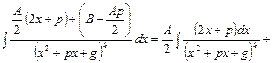
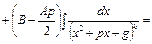
 Во втором интеграле выделим полный квадрат в знаменателе
Во втором интеграле выделим полный квадрат в знаменателе 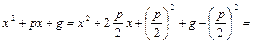
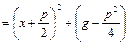 . Введем новую переменную
. Введем новую переменную 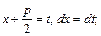
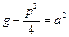
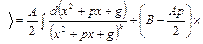
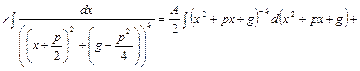
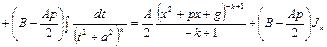 .
. берем по рекуррентной формуле (1).
берем по рекуррентной формуле (1).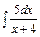 .
.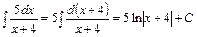 .
.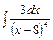 .
.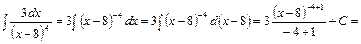

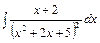 .
.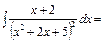
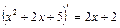 , тогда
, тогда 
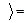
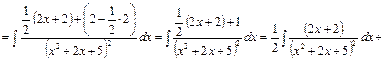
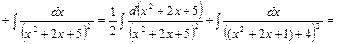
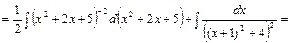

 ко второму интегралу применим рекуррентную формулу
ко второму интегралу применим рекуррентную формулу 
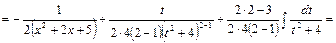
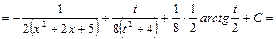
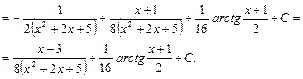
 , знаменатель которой разложен на множители
, знаменатель которой разложен на множители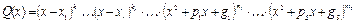 ,
,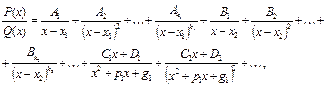
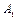 ,
, 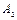 , …,
, …,  ,
,  , …,
, …,  ,
,  , …,
, …, 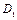 ,
, 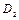 , … – некоторые действительные коэффициенты.
, … – некоторые действительные коэффициенты. будут соответствовать простейшие дроби I-II видов.
будут соответствовать простейшие дроби I-II видов.


