Вычисление статических моментов и координат центра тяжести плоской кривой
Пусть на плоскости Если массы распределены непрерывным образом вдоль некоторой кривой
где Координаты центра тяжести материальной плоской кривой
Пример 73. Найти координаты центра тяжести дуги кривой Решение. Для нахождения координат центра тяжести дуги кривой воспользуемся формулами
Так как кривая задана параметрическими уравнениями, то дифференциал дуги кривой найдем по формуле
Вычислим статические моменты относительно осей координат:
Координаты центра тяжести дуги кривой
Пример 74. Найти координаты центра тяжести кривой Решение. Кривая задана в полярной системе координат, поэтому дифференциал дуги кривой
Тогда Вычислим декартовы координаты через полярные:
Найдем статические моменты кривой относительно осей координат
Итак, координаты центра тяжести кривой
|
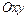задана система материальных точек 
, 
, …, 
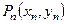с массами 
, 
, 
, …, 
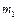. Произведения 
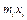и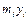 
называются статическими моментами массы 
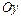относительно осей 
и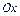 
.
, уравнение которой 
, то статические моменты кривой относительно осей координат будут вычисляться по формулам: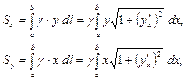
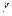– постоянная плотность однородной кривой 
: 
, 
(
).
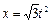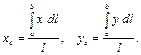
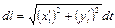, тогда длина дуги 
. Найдем
, 
,
.
.
.
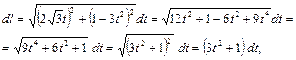
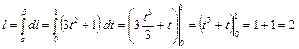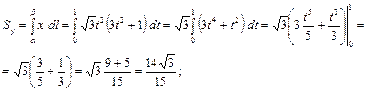
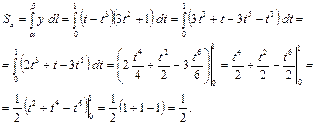
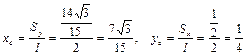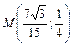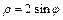, заключенной между лучам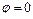и 
и 
.
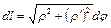и длина дуги кривой 
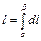. Найдем 
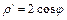и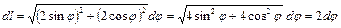
.
.
.
; 
.
.
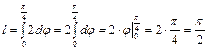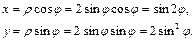
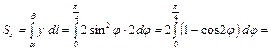
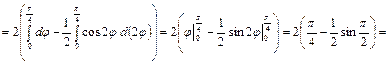
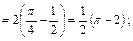
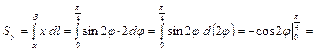
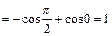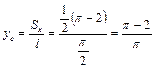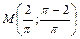