Обобщением определенного интеграла на случай функций двух переменных является двойной интеграл.
Пусть в замкнутой области  плоскости
плоскости  задана положительная непрерывная функция
задана положительная непрерывная функция  .
.
Определение: Часть пространства, ограниченная снизу замкнутой областью  , сверху поверхностью
, сверху поверхностью  , с боков цилиндрической поверхностью, образующие которой параллельны оси
, с боков цилиндрической поверхностью, образующие которой параллельны оси 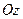 , а направляющий служит контур области
, а направляющий служит контур области  , называется цилиндрическим телом.
, называется цилиндрическим телом.
Найдем объем данного цилиндрического тела.
Разобьем область  на
на  элементарных областей
элементарных областей 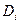 , площадь которых обозначим через
, площадь которых обозначим через 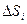 , а диаметры
, а диаметры 

|
Рисунок 1 – Плоская область 
|
В каждой области 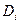 выберем произвольную точку
выберем произвольную точку  , найдем значение функции в этой точке
, найдем значение функции в этой точке  .
.
Рассмотрим цилиндрические столбики с основанием 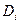 , ограниченные сверху кусками поверхности
, ограниченные сверху кусками поверхности  .
.

|
| Рисунок 2
|
В своей совокупности они составляют тело  . Объем цилиндрического столбика приближенно равен
. Объем цилиндрического столбика приближенно равен  , а объем цилиндрического тела:
, а объем цилиндрического тела:
 . (1)
. (1)
Эта сумма называется интегральной суммой функции  в области
в области  .
.
Равенство (1) тем точнее, чем больше  и чем меньше размеры элементарных областей
и чем меньше размеры элементарных областей 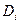 . Если
. Если  неограниченно возрастает, то за объем цилиндрического тела можно будет принять предел интегральной суммы:
неограниченно возрастает, то за объем цилиндрического тела можно будет принять предел интегральной суммы:
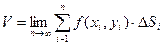
Определение: Если существует  , то он называется двойным интегралом от функции
, то он называется двойным интегралом от функции  по области
по области  и обозначается
и обозначается  , т.е.
, т.е.  .
.
где  - интегрируемая функция в области
- интегрируемая функция в области  ,
,
 - область интегрирования,
- область интегрирования,
 и
и  - переменные интегрирования,
- переменные интегрирования,
 или
или  - элемент площади.
- элемент площади.
Для всякой ли функции  существует двойной интеграл?
существует двойной интеграл?
Теорема 1 (достаточное условие интегрируемости функции). Если функция  непрерывна в замкнутой области
непрерывна в замкнутой области  , то она интегрируема в этой области.
, то она интегрируема в этой области.
Величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Если при любых 
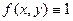 , то
, то  - площадь области
- площадь области  .
.
Рассмотрим задачу на нахождение массы плоской пластинки. Пусть требуется найти массу  плоской пластинки
плоской пластинки  , зная ее поверхностную плотность
, зная ее поверхностную плотность  . Функция
. Функция  - непрерывна в каждой точке области
- непрерывна в каждой точке области  .
.
Разобьем пластинку  на
на  элементарных частей
элементарных частей 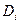 с площадями
с площадями 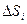 . В каждой области
. В каждой области 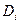 возьмем произвольную точку
возьмем произвольную точку  и вычислим в ней плотность
и вычислим в ней плотность  . Если в области
. Если в области 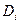 достаточно малы, то плотность можно считать постоянной и равной
достаточно малы, то плотность можно считать постоянной и равной  , а массу данной области
, а массу данной области  .
.
Тогда масса всей пластинки  будет приближенно равна
будет приближенно равна
 .
.
Точное значение массы пластинки  получим при условии, что
получим при условии, что  :
:
 или
или  .
.
Итак, двойной интеграл от функции  численно равен массе пластинки, если подынтегральную функцию
численно равен массе пластинки, если подынтегральную функцию  считать плотностью этой пластинки в точке
считать плотностью этой пластинки в точке  . В этом состоит физический смысл двойного интеграла.
. В этом состоит физический смысл двойного интеграла.

 плоскости
плоскости  задана положительная непрерывная функция
задана положительная непрерывная функция  .
.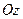 , а направляющий служит контур области
, а направляющий служит контур области  элементарных областей
элементарных областей 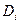 , площадь которых обозначим через
, площадь которых обозначим через 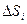 , а диаметры
, а диаметры 

 , найдем значение функции в этой точке
, найдем значение функции в этой точке 
 . Объем цилиндрического столбика приближенно равен
. Объем цилиндрического столбика приближенно равен  , а объем цилиндрического тела:
, а объем цилиндрического тела: . (1)
. (1) в области
в области 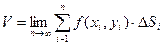
 , то он называется двойным интегралом от функции
, то он называется двойным интегралом от функции  , т.е.
, т.е.  .
. и
и  - переменные интегрирования,
- переменные интегрирования, или
или  - элемент площади.
- элемент площади.
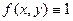 , то
, то  - площадь области
- площадь области  плоской пластинки
плоской пластинки  . Функция
. Функция  . Если в области
. Если в области  , а массу данной области
, а массу данной области  .
. .
. :
: или
или  .
. . В этом состоит физический смысл двойного интеграла.
. В этом состоит физический смысл двойного интеграла.


