Вычисление тройного интеграла в декартовых координатах.
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов. Пусть областью интегрирования является тело, ограниченное снизу поверхностью
Область
Тогда, если
При этом сначала вычисляется интеграл по переменной Результатом вычисления есть функция двух переменных Если область
, то переходя от двойного интеграла по области
Порядок интегрирования может быть изменен. Пример 8. Вычислить Решение.
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах. При вычислении тройного интеграла, как и двойного, часто применяются метод подстановки:
то справедлива формула замены переменных в тройном интеграле:
|

 , сверху - поверхностью
, сверху - поверхностью  , причем
, причем  ,
, 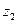 - непрерывные функции в замкнутой области
- непрерывные функции в замкнутой области  и
и 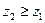 .
. .
. называется правильной в направлении оси
называется правильной в направлении оси 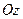 , если любая прямая, параллельная оси
, если любая прямая, параллельная оси 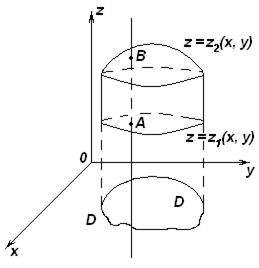
 непрерывна в области
непрерывна в области  .
. при постоянных
при постоянных  и
и  , а затем двойной интеграл. Нижней границей является аппликата точки
, а затем двойной интеграл. Нижней границей является аппликата точки  входа в область
входа в область  - точка выхода прямой из области
- точка выхода прямой из области  ,
,  ,
, 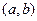 ,
,  и
и  , где
, где  и
и  - непрерывные на отрезке
- непрерывные на отрезке 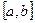 функции, причем
функции, причем 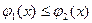

 .
. , где
, где  ,
,  ,
,  ,
,  .
.
 ,
,  ,
,  . Если данные функции имеют непрерывные частные производные и отличный от нуля определитель
. Если данные функции имеют непрерывные частные производные и отличный от нуля определитель ,
, .
. - якобиан преобразования.
- якобиан преобразования.


