Пусть на плоскости  задана непрерывная кривая
задана непрерывная кривая  (или
(или  ) длины
) длины  . В каждой точке дуги
. В каждой точке дуги  определена непрерывная функция
определена непрерывная функция  . Разобьем кривую
. Разобьем кривую  точками
точками  ,
,  ,
,  , …,
, …,  на
на  произвольных дуг
произвольных дуг  с длинами
с длинами  . На каждой дуге
. На каждой дуге  выберем произвольную точку
выберем произвольную точку 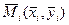 и составим интегральную сумму для функции
и составим интегральную сумму для функции  по кривой
по кривой  .
.
 (1)
(1)
Пусть  - наибольшая из длин дуг.
- наибольшая из длин дуг.
Определение 1. Если при  (
(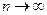 ) существует конечный предел интегральных сумм (1), то его называют криволинейным интегралом от функции
) существует конечный предел интегральных сумм (1), то его называют криволинейным интегралом от функции  по длине дуги кривой
по длине дуги кривой 
(или I рода) и обозначают 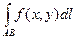 или
или 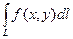 , т.е.
, т.е.
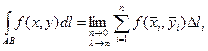 (2)
(2)
Теорема 2 (условие существования криволинейного интеграла I рода). Если функция  непрерывна в каждой точке гладкой кривой, то криволинейный интеграл I рода существует и его величина не зависит ни от способа разбиения кривой на части, ни от выбора точек в них.
непрерывна в каждой точке гладкой кривой, то криволинейный интеграл I рода существует и его величина не зависит ни от способа разбиения кривой на части, ни от выбора точек в них.
Аналогично вводится понятие криволинейного интеграла по пространственной кривой.
Основные свойства.
1. Криволинейный интеграл не зависит от направления пути интегрирования.
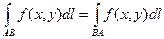 .
.
2. Постоянный множитель можно вынести за знак интеграла.
 ,
,  .
.
3.  .
.
4. 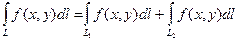 ,
,  .
.
5. Если для всех точек кривой  , то
, то
 .
.
6.  - длина дуги
- длина дуги  .
.
7. Теорема о среднем.
Если функция  непрерывна на кривой
непрерывна на кривой  , то найдется такая точка
, то найдется такая точка  , что
, что
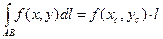 .
.
Вычисление криволинейного интеграла I рода.
Вычисление криволинейного интеграла I рода сводится к вычислению определенного интеграла.
1. Кривая  задана в прямоугольной системе координат уравнением
задана в прямоугольной системе координат уравнением 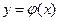 ,
, 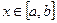 ,
,  - непрерывно дифференцируемая функция.
- непрерывно дифференцируемая функция.
Дифференциал дуги кривой  , тогда
, тогда
 (3)
(3)
Пример 11. Вычислить  , где
, где  - парабола
- парабола  ,
,  .
.
Решение.
1) Найдем  :
:
 ;
;
2) Найдем  :
:
 .
.
3) Вычислим интеграл:
 .
.
2. Кривая  задана параметрическими уравнениями
задана параметрическими уравнениями  ,
, 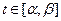 , где
, где  и
и  - непрерывно дифференцируемые функции.
- непрерывно дифференцируемые функции.
Дифференциал дуги кривой  , тогда
, тогда
 (4)
(4)
Аналогично для пространственной кривой  ,
,  ,
,  :
:
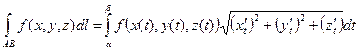 (5)
(5)
Пример 12. Вычислить  вдоль кривой
вдоль кривой 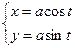 , если
, если  .
.
Решение.
1) Найдем  и
и  :
:
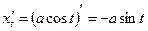 ,
,
 .
.
2) Найдем  :
:
 .
.
3) Вычислим
 .
.
3. Кривая  задана в полярной системе координат уравнением
задана в полярной системе координат уравнением
 ,
,  .
.
Дифференциал дуги кривой  , тогда
, тогда
 (6) Пример 13. Вычислить
(6) Пример 13. Вычислить  , где
, где  - лепесток лемнискаты
- лепесток лемнискаты  , расположенный в I четверти.
, расположенный в I четверти.
Решение.
1) Найдем  :
:
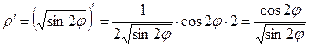 .
.
2) Найдем  :
:

 .
.
 .
.
3) Вычислим.



Приложения криволинейного интеграла I рода.
1. Длина дуги кривой
 (7)
(7)
2. Площадь цилиндрической поверхности
Если направляющей цилиндрической поверхности служит кривая  , лежащая в плоскости
, лежащая в плоскости  , а образующая параллельна оси
, а образующая параллельна оси 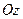 , то площадь данной поверхности, задаваемой функцией
, то площадь данной поверхности, задаваемой функцией  , находится по формуле
, находится по формуле
 (8)
(8)
3. Масса кривой
Пусть  определяет плотность кривой в каждой ее точке
определяет плотность кривой в каждой ее точке  , тогда
, тогда
 ,
,
а масса всей кривой
 ,
,
точнее значение массы получим, если перейдем к пределу при 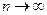 :
:
 (9)
(9)
4. Статические моменты, центр тяжести дуги кривой
 ,
,  ,
,  ,
,  .
.
5. Моменты инерции
 ,
,  ,
, 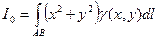 .
.

 задана непрерывная кривая
задана непрерывная кривая  (или
(или  ) длины
) длины  . В каждой точке дуги
. В каждой точке дуги  . Разобьем кривую
. Разобьем кривую  ,
,  ,
,  , …,
, …,  на
на  произвольных дуг
произвольных дуг  с длинами
с длинами  . На каждой дуге
. На каждой дуге 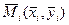 и составим интегральную сумму для функции
и составим интегральную сумму для функции  (1)
(1) - наибольшая из длин дуг.
- наибольшая из длин дуг. (
(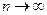 ) существует конечный предел интегральных сумм (1), то его называют криволинейным интегралом от функции
) существует конечный предел интегральных сумм (1), то его называют криволинейным интегралом от функции 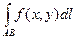 или
или 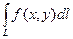 , т.е.
, т.е.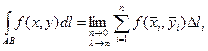 (2)
(2)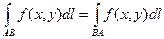 .
. ,
,  .
. .
.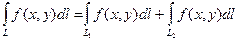 ,
,  .
. , то
, то .
. - длина дуги
- длина дуги  , что
, что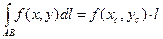 .
.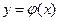 ,
, 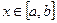 ,
,  - непрерывно дифференцируемая функция.
- непрерывно дифференцируемая функция. , тогда
, тогда (3)
(3) , где
, где  ,
,  .
. :
: ;
; :
: .
. .
. ,
, 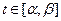 , где
, где  и
и  - непрерывно дифференцируемые функции.
- непрерывно дифференцируемые функции. , тогда
, тогда (4)
(4) :
: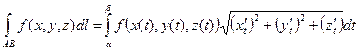 (5)
(5) вдоль кривой
вдоль кривой 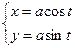 , если
, если  .
. и
и  :
: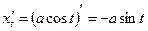 ,
, .
. .
. .
. ,
,  .
. , тогда
, тогда (6) Пример 13. Вычислить
(6) Пример 13. Вычислить  , где
, где  , расположенный в I четверти.
, расположенный в I четверти. :
: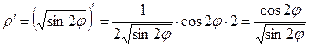 .
.
 .
. .
.


 (7)
(7)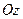 , то площадь данной поверхности, задаваемой функцией
, то площадь данной поверхности, задаваемой функцией  , находится по формуле
, находится по формуле (8)
(8) определяет плотность кривой в каждой ее точке
определяет плотность кривой в каждой ее точке  , тогда
, тогда ,
, ,
, (9)
(9) ,
,  ,
,  ,
,  .
. ,
,  ,
, 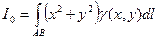 .
.


