Вычисление статических моментов и координат центра тяжести плоской фигуры
Пусть дана материальная плоская область, ограниченная кривой
Поверхностная плотность во всех точках пластинки постоянна и равна Статические моменты пластинки относительно осей координат определяют по формулам
а координаты центра тяжести равны
Если материальная плоская фигура ограничена линиями
Тогда координаты центра тяжести плоской фигуры находятся по формулам
Пример 75. Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями
Решение. Так как фигура однородна и симметрична относительно оси Найдем координаты точек
Найдем массу плоской пластинки, ограниченной линиями
то есть
Далее найдем статический момент относительно оси
то есть
Тогда координаты центра тяжести будут равны
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ 1. Определение первообразной функции. Геометрический смысл совокупности первообразных функций. 2. Определение неопределенного интеграла. 3. Таблица основных интегралов. 4. Свойства неопределенного интеграла. 5. Основные методы интегрирования: – метод непосредственного интегрирования; – метод подведения под знак дифференциала; – метод интегрирования подстановкой; – метод интегрирования по частям; – метод интегрирования дробей, содержащих квадратный трехчлен в знаменателе; – интегрирование простейших рациональных дробей I-IV типов; – разложение правильной рациональной дроби на простейшие дроби. Интегрирование рациональной дроби; – интегрирование иррациональных функций; – интегрирование тригонометрических функций. 6. Определение определенного интеграла, его геометрический и физический смыслы. 7. Свойства определенного интеграла. 8. Вычисление определенного интеграла. Формула Ньютона-Лейбница. 9. Формула замены переменной в определенном интеграле. 10. Формула интегрирования по частям в определенном интеграле. 11. Определение несобственного интеграла первого рода. 12. Определение несобственного интеграла второго рода. 13. Вычисление площади плоской фигуры. 14. Вычисление длины дуги кривой. 15. Вычисление объема тела вращения. 16. Вычисление площади поверхности вращения. 17. Вычисление статических моментов и координат центра тяжести дуги кривой. 18. Вычисление статических моментов и координат центра тяжести плоской фигуры. 19. Вычисление работы переменной силы. 20. Вычисление пути, пройденного телом за промежуток времени. 21. Вычисление давления жидкости на вертикальную пластинку.
ЛИТЕРАТУРА 1. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учебник для втузов/ Н.С. Пискунов – М.: Наука, 1985. – т.1, 2. 2. Бугров, Я.С. Дифференциальное и интегральное исчисления/ Я.С. Бугров, С.М. Никольский – М.: Наука, 1984. 3. Данко, П.Е. Высшая математика в упражнениях и задачах/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова – М.: Высшая школа, 1999. – часть 1, 2. 4. Мышкис, А.Д. Лекции по высшей математике/ А.Д. Мышкис – М.: Наука, 1969. 5. Красс, М.С. Основы математики и ее приложения в экономическом образовании: учебник/ М.С. Красс, Б.П. Чупрынов – М.: Дело, 2000.
|

 и прямыми
и прямыми 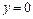 ,
,  ,
,  (рисунок 22).
(рисунок 22).
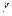 . Тогда масса всей пластинки равна
. Тогда масса всей пластинки равна  .
. ,
,  ,
, ,
, 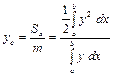 .
. и
и  ,
, 
 .
.
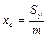 и
и  или
или ,
, .
.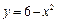 и
и  (рисунок 24).
(рисунок 24).
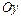 , то центр тяжести будет расположен на оси
, то центр тяжести будет расположен на оси 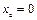 .
.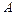 и
и  :
: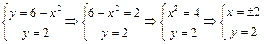 ;
; ,
, 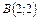 .
. ,
,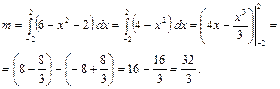
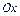
 ,
,
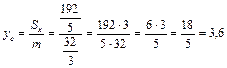 ;
; .
.


