Вычисление двойного интеграла в декартовых координатах
Вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов. Пусть требуется вычислить двойной интеграл
Пусть область
Постоим сечение цилиндрического тела плоскостью, перпендикулярной оси
В сечении получим криволинейную трапецию Площадь данной трапеции находим с помощью определенного интеграла
Согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
Объем цилиндрического тела можно вычислить с помощью двойного интеграла
Данное равенство можно записать в идее:
Правую часть формулы (2) называют двукратным или повторным интегралом от функции Интеграл При вычислении двукратного интеграла сначала берем внутренний интеграл, считая Если область
В данном случае, при вычислении внутреннего интеграла, считаем Нужно помнить, что пределы внешнего интеграла всегда постоянны. Пример 1. Вычислить Решение. Изобразим область интегрирования
Найдем точку пересечения кривых
Тогда Для вычисления данного интеграла воспользуемся формулой (3), т.е. спроектируем область
При вычислении данного интеграла по формуле (2) нужно область Область
Получили тот же результат. Если область
т.е. двойной интеграл не зависит от порядка интегрирования.
Вопросы для самоконтроля 1. Что такое интегральная сумма для функции 2. Что называется двойным интегралом от функции 3. Геометрический смысл двойного интеграла. 4. Физический смысл двойного интеграла. 5. Какая область 6. Как вычислить двойной интеграл в декартовых координатах? 7. Как изменить порядок интегрирования в двойном интеграла?
|

 , где функция
, где функция  непрерывна в области
непрерывна в области  . Как известно, двойной интеграл выражает объем цилиндрического тела. Найдем этот объем, используя метод параллельных сечений:
. Как известно, двойной интеграл выражает объем цилиндрического тела. Найдем этот объем, используя метод параллельных сечений: , где
, где  - площадь сечения плоскостью, перпендикулярной оси
- площадь сечения плоскостью, перпендикулярной оси 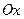 , а
, а  ,
,  - уравнение плоскостей, ограничивающих данное тело.
- уравнение плоскостей, ограничивающих данное тело. и
и  , причем функции
, причем функции  и
и  непрерывны и
непрерывны и 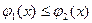 для
для  . Область
. Область  .
.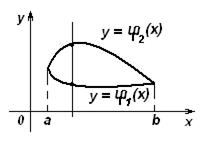
 , где
, где 
 , ограниченную линиями
, ограниченную линиями  , где
, где  ,
,  .
. .
.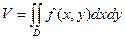 . Следовательно,
. Следовательно, .
. (2)
(2) называют внутренним интегралом.
называют внутренним интегралом. постоянным, а затем внешний интеграл, результат внутреннего интеграла интегрируем по переменной
постоянным, а затем внешний интеграл, результат внутреннего интеграла интегрируем по переменной  до
до  .
. и
и 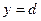 , кривыми
, кривыми  и
и  , причем
, причем  для всех
для всех  , т.е. область
, т.е. область 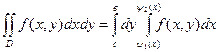 (3)
(3) постоянным.
постоянным. , где область
, где область  ,
,  ,
,  .
.
 :
: .
. и
и  . Нашей области
. Нашей области  .
. , тогда
, тогда  и
и  .
.


 на две область
на две область  и
и  , тогда
, тогда  .
. .
.




 ,
,


