Приложение двойного интеграла.
1. Объем тела. Объем цилиндрического тела находится по формуле
где 2. Площадь плоской фигуры. Если подынтегральная функция
В полярных координатах
2’. Вычисление площади поверхности. 1. Если гладкая поверхность задана уравнением
где 2. Если гладкая поверхность задана уравнением
где 3. Масса плоской пластинки
4. Статические моменты и координаты центра тяжести плоской пластинки. Статические моменты относительно осей координат:
Координаты центра тяжести
5. Моменты инерции плоской фигуры. Моментом инерции материальной точки массы
Моменты инерции плоской фигуры относительно осей
Момент инерции относительно начала координат:
Пример 4. Вычислить объем тела, ограниченного поверхностями Решение. Изобразим тело, объем которого нужно вычислить.
Найдем объем тела по формуле
Пример 5. Найти площадь пластинки, ограниченной линиями Решение. Изобразим область
Найдем точки пересечения кривых:
Область Площадь вычислим по формуле
Пример 6. Вычислить площадь части поверхности Пример 7. Найти координаты центра тяжести плоской пластинки, ограниченной линиями
Вопросы для самоконтроля 1. Что такое Якобиан перехода и чему он равен в полярных координатах? 2. Выражение двойного интеграла в полярных координатах. 3. Как вычислить объем цилиндрического тела? 4. Как вычислить площадь плоской пластинки? 5. Как найти площадь поверхности? 6. Как вычислить массу пластинки? 7. Как найти координаты центра тяжести пластинки? 8. Как найти моменты инерции плоской фигуры относительно осей
|

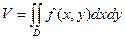 ,
, - уравнение поверхности, ограничивающей тело сверху.
- уравнение поверхности, ограничивающей тело сверху.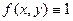 , то получим формулу для вычисления площади плоской области
, то получим формулу для вычисления площади плоской области  :
: .
. .
. ,
, .
. , то
, то ,
, .
. .
. ,
,  .
. ,
,  .
. называется произведение массы
называется произведение массы  точки до оси:
точки до оси: .
.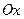 и
и  могут быть вычислены по формулам:
могут быть вычислены по формулам: ,
, .
. .
. ,
,  ,
,  ,
,  ,
,  .
.

 (ед. куб.).
(ед. куб.). ,
,  .
.

 и
и  .
. .
.
 (кв. ед.).
(кв. ед.).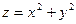 , вырезанной цилиндром
, вырезанной цилиндром  и расположенной в I октанте.
и расположенной в I октанте. ,
,  ,
,  ,
,  .
.


