Задание. 2. Вычислить , где - внутренность треугольника с вершинами ,
2. Вычислить 2. Изменить порядок интегрирования в двойном интеграле Литература 1. Н.С. Пискунов «Дифференциальное и интегральное исчисления» ч.2., гл. XIV, § 1 – 3. 2. П.Е. Данко «Высшая математика в упражнениях и задачах» ч.2., гл. I, § 1. п 4. Вычисление двойного интеграла в полярных координатах.
Для упрощения вычисления двойного интеграла часто применяют метод подстановки, т.е. вводят новые переменные под знак двойного интеграла. Пусть
Функция
Определитель Чаще всего при вычислении двойного интеграла переходят к полярным координатам Вычислим Якобиан перехода к полярным координатам
Тогда
где
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведение его к двукратному интегралу. Пусть область
При вычислении внутреннего интеграла Замечание. Переход к полярным координатам полезен тогда, когда область интегрирования есть круг или его часть и когда подынтегральная функция содержит выражение Пример 2. Вычислить двойной интеграл Решение. 1. Изобразим область
2. Перейдем к полярным координатам 3. Найдем пределы интегрирования: 4. Вычислим интеграл
Пример 3. Вычислить
|

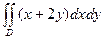 , где
, где  - внутренность треугольника с вершинами
- внутренность треугольника с вершинами  ,
,  ,
,  .
.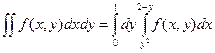 .
. ,
,  , причем данные функции имеют непрерывные частные производные первого порядка в области
, причем данные функции имеют непрерывные частные производные первого порядка в области  плоскости
плоскости  и отличный от нуля определитель
и отличный от нуля определитель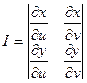 (4)
(4) непрерывна в области
непрерывна в области  (5)
(5) называется определителем Якоби (немецкий математик) или Якобианом.
называется определителем Якоби (немецкий математик) или Якобианом. ,
,  .
. .
.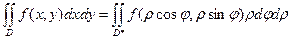 , (6)
, (6)
 и
и  , кривыми
, кривыми  и
и  . Если луч, выходящий из полюса пересекает границу области
. Если луч, выходящий из полюса пересекает границу области  . (7)
. (7) считаем постоянным.
считаем постоянным. .
. , если область
, если область  и осью
и осью 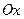 .
.
 .
. ,
, 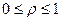 .
.

 , если область
, если область  .
.


