Из геометрического смысла определенного интеграла следует, что площадь криволинейной трапеции, ограниченной сверху кривой  , снизу отрезком
, снизу отрезком 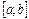 оси
оси 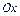 , справа и слева прямыми
, справа и слева прямыми  и
и  (рисунок 8), находится по формуле
(рисунок 8), находится по формуле
 .
.

| 
|
| Рисунок 8 – Криволинейная трапеция
| Рисунок 9 – Фигура, ограниченная линиями  , ,  , ,  
|
Если криволинейная трапеция расположена ниже оси 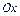 , то есть
, то есть  (рисунок 9), то площадь может быть найдена по формуле
(рисунок 9), то площадь может быть найдена по формуле
 .
.
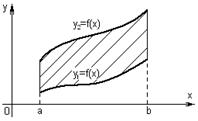
Площадь фигуры, ограниченной кривыми  и
и 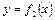 (
( для любого
для любого 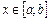 ), прямыми
), прямыми  и
и  (рисунок 10), можно найти по формуле
(рисунок 10), можно найти по формуле
 .
.
| 
|
Рисунок 10 – Фигура, ограниченная линиями  , ,  , ,  и и 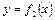
| Рисунок 11 – Криволинейная трапеция, расположенная относительно оси 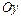
|
Если криволинейная трапеция ограничена справа непрерывной кривой  , слева отрезком
, слева отрезком  оси
оси 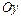 , снизу и сверху прямыми
, снизу и сверху прямыми 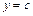 и
и  (рисунок 11), то ее площадь находится по формуле
(рисунок 11), то ее площадь находится по формуле
 .
.
Если криволинейная трапеция ограничена кривой, заданной параметрическими уравнениями
 ,
,
то ее площадь находится по формуле
 .
.
Пример 60. Найти площадь фигуры, ограниченной линиями 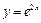 ,
, 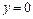 ,
,  ,
, 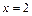 (рисунок 12).
(рисунок 12).

|
| Рисунок 12 – Криволинейная трапеция
|
Решение. Для нахождения площади криволинейной трапеции, ограниченной заданными линиями, воспользуемся формулой  :
:

 (кв.ед.)
(кв.ед.)
Пример 61. Найти площадь фигуры, ограниченной линиями 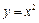 и
и  (рисунок 13).
(рисунок 13).

|
Рисунок 13 – Изображение плоской фигуры, ограниченной линиями 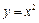 и и 
|
Решение. Найдем точки пересечения данных кривых
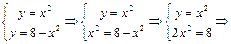

Таким образом, точки пересечения  и
и  .
.
Фигура, ограниченная параболами 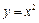 и
и  , симметрична относительно оси
, симметрична относительно оси 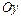 , поэтому достаточно вычислить половину площади данной фигуры и полученный результат умножить на 2. Для нахождения площади воспользуемся формулой
, поэтому достаточно вычислить половину площади данной фигуры и полученный результат умножить на 2. Для нахождения площади воспользуемся формулой  :
:
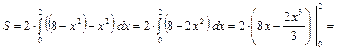
 (кв.ед.).
(кв.ед.).
Пример 62. Вычислить площадь фигуры, ограниченной эллипсом  ,
, 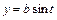 (рисунок 14).
(рисунок 14).

|
| Рисунок 14 – Эллипс
|
Решение. Найдем площадь  области и полученный результат умножим на 4.
области и полученный результат умножим на 4.
Воспользуемся формулой  . Так как
. Так как  изменяется от 0 до
изменяется от 0 до  , то
, то  изменяется от
изменяется от  до
до  , тогда
, тогда

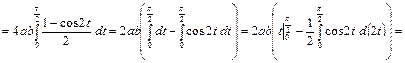
 (кв.ед.).
(кв.ед.).

 , снизу отрезком
, снизу отрезком 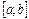 оси
оси 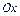 , справа и слева прямыми
, справа и слева прямыми  и
и  (рисунок 8), находится по формуле
(рисунок 8), находится по формуле .
.


 (рисунок 9), то площадь может быть найдена по формуле
(рисунок 9), то площадь может быть найдена по формуле .
. и
и 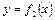 (
( для любого
для любого 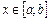 ), прямыми
), прямыми  .
.

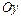
 , слева отрезком
, слева отрезком  оси
оси 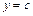 и
и  (рисунок 11), то ее площадь находится по формуле
(рисунок 11), то ее площадь находится по формуле .
. ,
, .
.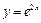 ,
, 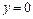 ,
,  ,
, 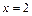 (рисунок 12).
(рисунок 12).

 (кв.ед.)
(кв.ед.)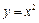 и
и  (рисунок 13).
(рисунок 13).
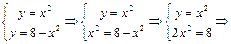

 и
и  .
.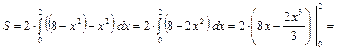
 (кв.ед.).
(кв.ед.). ,
, 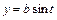 (рисунок 14).
(рисунок 14).
 области и полученный результат умножим на 4.
области и полученный результат умножим на 4. изменяется от 0 до
изменяется от 0 до  , то
, то  изменяется от
изменяется от  до
до  , тогда
, тогда
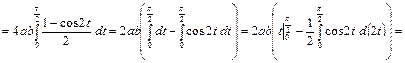
 (кв.ед.).
(кв.ед.).


