При рассмотрении определенного интеграла предполагалось, что подынтегральная функция является ограниченной на  . В том случае, когда функция не является ограниченной, задача интегрирования формулируется иначе.
. В том случае, когда функция не является ограниченной, задача интегрирования формулируется иначе.
Определение 10. Пусть функция  определена и непрерывна в
определена и непрерывна в  ,
,  и стремится к бесконечности при
и стремится к бесконечности при  . Составим интеграл
. Составим интеграл
 .
.
Предел этого интеграла при  называется несобственным интегралом второго рода (или интегралом от неограниченной функции) на интервале
называется несобственным интегралом второго рода (или интегралом от неограниченной функции) на интервале 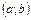 :
:
 .
.
Если предел существует и конечен, то несобственный интеграл 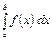 сходится. Если предел не существует или бесконечен, то говорят, что интеграл
сходится. Если предел не существует или бесконечен, то говорят, что интеграл 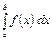 расходится.
расходится.
Если 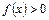 , то несобственный интеграл второго рода
, то несобственный интеграл второго рода 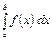 (разрыв в точке
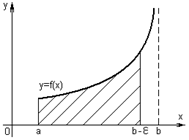
(разрыв в точке  ) равен площади бесконечно высокой криволинейной трапеции (рисунок 7).
) равен площади бесконечно высокой криволинейной трапеции (рисунок 7).
|
| Рисунок 7 – Геометрическая иллюстрация несобственного интеграла второго рода
|
Если функция  имеет бесконечный разрыв в точке
имеет бесконечный разрыв в точке  , то
, то
 .
.
Если функция  имеет разрыв во внутренней точке
имеет разрыв во внутренней точке 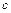 отрезка
отрезка 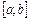 , то несобственный интеграл второго рода имеет вид:
, то несобственный интеграл второго рода имеет вид:
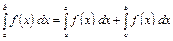 .
.
Интеграл 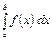 сходится, если оба несобственных интеграла
сходится, если оба несобственных интеграла 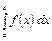 и
и 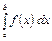 сходятся.
сходятся.
Пример 55. Вычислить интеграл или доказать его расходимость 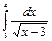 .
.
Решение. Подынтегральная функция не определена в точке  . По определению несобственного интеграла второго рода имеем
. По определению несобственного интеграла второго рода имеем
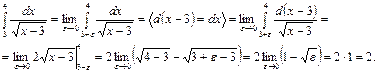
Так как существует конечный предел, то данный интеграл сходится и равен 2, то есть  .
.
Пример 56. Вычислить интеграл или доказать его расходимость  .
.
Решение. Функция на отрезке  не определена в точке
не определена в точке 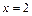 . По определению имеем
. По определению имеем

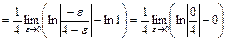
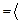 если
если  , то
, то  .
.
Следовательно,  расходится.
расходится.
Пример 57. Вычислить интеграл или доказать его расходимость 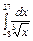 .
.
Решение. Функция  терпит разрыв во внутренней точке отрезка
терпит разрыв во внутренней точке отрезка 
 . Поэтому данный интеграл представим в виде суммы двух несобственных интегралов
. Поэтому данный интеграл представим в виде суммы двух несобственных интегралов
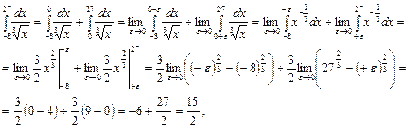
то есть  сходится.
сходится.
Аналогично можно показать, что интегралы  ,
, 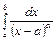 ,
, 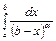 сходятся при
сходятся при 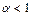 и расходятся при
и расходятся при  .
.
Данные интегралы используются в признаке сравнения в качестве эталонных.
Не всегда удается выяснить сходимость несобственных интегралов второго рода с помощью определения, поэтому используют признаки сравнения.
Теорема 13. Если на промежутке  функции
функции  и
и 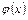 непрерывны и удовлетворяют условию
непрерывны и удовлетворяют условию  , а при
, а при  терпят бесконечный разрыв, то:
терпят бесконечный разрыв, то:
1) из сходимости интеграла  следует сходимость интеграла
следует сходимость интеграла 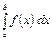 ;
;
2) из расходимости интеграла 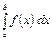 следует расходимость интеграла
следует расходимость интеграла  .
.
Теорема 14. Если функции  и
и 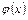 непрерывны на промежутке
непрерывны на промежутке  , в точке
, в точке  терпят бесконечный разрыв, и существует предел
терпят бесконечный разрыв, и существует предел  ,
, 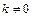 , то интегралы
, то интегралы 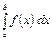 и
и  одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Пример 58. Вычислить интеграл или доказать его расходимость  .
.
Решение. Подынтегральная функция терпит разрыв в точке  . При
. При  функции
функции 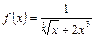 и
и  удовлетворяют условию
удовлетворяют условию  , а интеграл
, а интеграл
 –
–
сходится, значит и исходный интеграл  сходится.
сходится.
Пример 59. Вычислить интеграл или доказать его расходимость 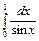 .
.
Решение. Функция 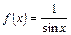 имеет разрыв в точке
имеет разрыв в точке  . Рассмотрим функцию
. Рассмотрим функцию  , которая также терпит разрыв в точке
, которая также терпит разрыв в точке  . Интеграл
. Интеграл  , то есть интеграл расходится. Найдем предел
, то есть интеграл расходится. Найдем предел
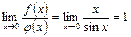 ,
,
то есть 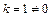 , значит и исходный интеграл
, значит и исходный интеграл 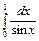 – расходится.
– расходится.

 . В том случае, когда функция не является ограниченной, задача интегрирования формулируется иначе.
. В том случае, когда функция не является ограниченной, задача интегрирования формулируется иначе. определена и непрерывна в
определена и непрерывна в  ,
,  и стремится к бесконечности при
и стремится к бесконечности при  . Составим интеграл
. Составим интеграл .
. называется несобственным интегралом второго рода (или интегралом от неограниченной функции) на интервале
называется несобственным интегралом второго рода (или интегралом от неограниченной функции) на интервале 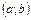 :
: .
.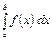 сходится. Если предел не существует или бесконечен, то говорят, что интеграл
сходится. Если предел не существует или бесконечен, то говорят, что интеграл 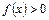 , то несобственный интеграл второго рода
, то несобственный интеграл второго рода  ) равен площади бесконечно высокой криволинейной трапеции (рисунок 7).
) равен площади бесконечно высокой криволинейной трапеции (рисунок 7).
 , то
, то .
.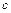 отрезка
отрезка 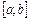 , то несобственный интеграл второго рода имеет вид:
, то несобственный интеграл второго рода имеет вид: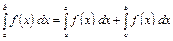 .
.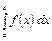 и
и 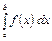 сходятся.
сходятся.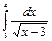 .
. . По определению несобственного интеграла второго рода имеем
. По определению несобственного интеграла второго рода имеем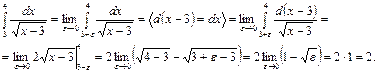
 .
. .
. не определена в точке
не определена в точке 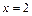 . По определению имеем
. По определению имеем
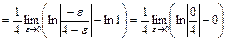
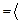 если
если  , то
, то  .
.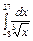 .
. терпит разрыв во внутренней точке отрезка
терпит разрыв во внутренней точке отрезка 
 . Поэтому данный интеграл представим в виде суммы двух несобственных интегралов
. Поэтому данный интеграл представим в виде суммы двух несобственных интегралов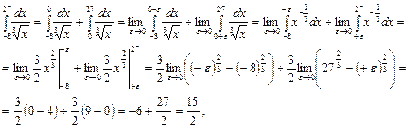
 сходится.
сходится. ,
, 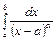 ,
, 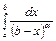 сходятся при
сходятся при  и расходятся при
и расходятся при  .
. функции
функции 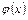 непрерывны и удовлетворяют условию
непрерывны и удовлетворяют условию  , а при
, а при  следует сходимость интеграла
следует сходимость интеграла  ,
, 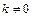 , то интегралы
, то интегралы  .
. функции
функции 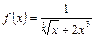 и
и  удовлетворяют условию
удовлетворяют условию  , а интеграл
, а интеграл –
–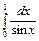 .
.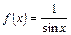 имеет разрыв в точке
имеет разрыв в точке  , которая также терпит разрыв в точке
, которая также терпит разрыв в точке  , то есть интеграл расходится. Найдем предел
, то есть интеграл расходится. Найдем предел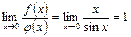 ,
,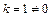 , значит и исходный интеграл
, значит и исходный интеграл 


