Домашнее задание №6.
Выполнить задания: 1. Найти общее решение дифференциального уравнения (x+1)dy – (y+1)dx=0 и частное решение, удовлетворяющее условию y= 1 при x=-1. 2. Найти общее решение дифференциального уравнения 3. Скорость гибели некоторых бактерий пропорциональна количеству бактерий N в данный момент времени t. Установить зависимость изменения количества бактерий от времени N(t), если константа убыли численности бактерий равна b. 4. Скорость растворения некоторого лекарственного вещества в таблетках пропорциональна количеству лекарства в таблетке. Найти закон растворения таблетки (т.е. закон изменения массы), если период полурастворения таблетки T. 5. Проверить постановкой, что данная функция является общим решением данного дифференциального уравнения: Самоподготовка (изучить и законспектировать по учебнику Ю.В. Морозова «Основы высшей математики и статистики» М., 1998, стр. стр. 95-102 ): Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами, их решение. Занятие №7. Дифференциальные уравнения II порядка. Решение задач с помощью дифференциальных уравнений Теоретические вопросы. 1. Понятие дифференциального уравнения. 2. Дифференциальные уравнения первого порядка с разделяющимися переменными. Их решение. 3. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами, их решение. Литература для подготовки: 3) Ю.В. Морозов «Основы высшей математики и статистики» М., 1998, стр. 95-102. 4) М.С. Федорова «Методическая разработка для самостоятельной подготовки по курсу «Высшая математика и информатика» для студентов лечебного и медико-профилактического факультетов», М., 2002. Самостоятельная работа: 1. Концентрация раствора изменяется с расстоянием по закону C=C0 2. Вычислите На практическом занятии выполнить задания из [1]: 1. Решить линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: V, № 1-5 2. Решить задачи из [2], стр. 32, раздел II. 3. Решить задачи: а) Груз массой 40 г колеблется на пружине, коэффициент жесткости которой k=0,36 н/м. Силу трения не учитывать. В начальный момент отсчета времени груз сместили на расстояние х0=4 см от положения равновесия, растянув пружину, и отпустили к нулевой начальной скорости. Определить: · закон отклонения груза; · отклонение груза от положения равновесия в момент t=p/3; · частоту колебаний груза. Решить предыдущую задачу при условии наличия силы трения, v-скорость движения груза. Определить закон движения груза, начертить график движения груза. 4. Найти общее решение дифференциального уравнения 5. Найти общее решение дифференциального уравнения 6. Решить дифференциальные уравнения.
|

 и подстановкой проверить правильность найденного решения. Найти частное решение при x=1, y=2.
и подстановкой проверить правильность найденного решения. Найти частное решение при x=1, y=2. для 2Y
для 2Y  .
. где C0 – некоторая постоянная величина. Получить формулу для градиента концентрации.
где C0 – некоторая постоянная величина. Получить формулу для градиента концентрации.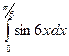
 и частное решение, удовлетворяющее условию y= -10 при x=16.
и частное решение, удовлетворяющее условию y= -10 при x=16. и подстановкой проверить правильность найденного решения. Найти частное решение при x=0, y=5.
и подстановкой проверить правильность найденного решения. Найти частное решение при x=0, y=5. , при y(0)= -3, y¢(0)=0.
, при y(0)= -3, y¢(0)=0.
 , при y(0)=0, y¢(0)=1.
, при y(0)=0, y¢(0)=1.
 , при y(1)=10, y¢(1)=2.
, при y(1)=10, y¢(1)=2.



