Численное решение нелинейных уравнений.

• Парасимпатическая система оказывает выраженное влияние на следующие органы (несколько ответов):

– потовые железы

– гладкая мускулатура кожных сосудов

– желудок

– бронхи

– сердце

 

 

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

 

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

 

 

Кафедра прикладной математики

 

ЧИСЛЕННЫЕ МЕТОДЫ

 

Часть 1

 

 

Методические указания к лабораторным и самостоятельным работам

по курсам «Информатика» и «Вычислительная математика»

 

Казань

 

УДК 621.313: 518.6

ББК 32.81

 

 

А95 Численные методы. Часть 1: Методические указания к лабораторным и самостоятельным работам по курсам «Информатика» и «Вычислительная математика». / Сост.: Ф.Г.Ахмадиев, Ф.Г.Габбасов, Р.Ф.Гиззятов, И.В.Маланичев. – Казань: Изд-во Казанск. гос. архитект.-строит. ун-та, 2013. – 34 с.

 

 

Печатается по решению Редакционно-издательского совета Казанского государственного архитектурно-строительного университета.

 

Методические указания состоят из двух частей и предназначены для выполнения лабораторных и самостоятельных работ студентами всех специальностей и направлений подготовки дневного и заочного отделений. В данной части приводятся численные методы решения нелинейных уравнений, систем линейных и нелинейных уравнений.

 

 

Рецензент

Доктор физико-математических наук, профессор КГАСУ

Р.Б.Салимов

 

 

УДК 621.313: 518.6

ББК 32.81

 

 

ã	Казанский государственный архитектурно-строительный университет, 2013
ã	Ахмадиев Ф.Г., Габбасов Ф.Г., Гиззятов Р.Ф., Маланичев И.В.,

 

Численное решение нелинейных уравнений.

Задана непрерывная функция . Требуется определить корни уравнения . Такая задача встречается в различных областях научных исследований, в том числе и при расчетах строительных конструкций, организации и управлении строительным производством.

Нелинейные уравнения можно разделить на два класса - алгебраические и трансцендентные. Алгебраическими уравнениями называются уравнения, содержащие только алгебраические функции. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.), называются трансцендентными.

Методы решения уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного соотношения. Если не удается решить уравнения прямыми методами, то для их решения используются итерационные методы, т.е. методы последовательных приближений. Алгоритм нахождения корня уравнения с помощью итерационного метода состоит из двух этапов:

а) отыскания приближенного значения корня или содержащего его отрезка;

б) уточнения значения до некоторой степени точности.

Приближенное значение корня (начальное приближение) может быть найдено различными способами из физических соображений, из решения аналогичной задачи при других исходных данных, с помощью графических методов. Если такие простые оценки исходного приближения произвести не удается, то находят две близко расположенные точки и , в которых непрерывная функция принимает значения разных знаков, т.е. . В этом случае между точками и есть, по крайней мере, одна точка, в которой . В качестве начального приближения первой итерации можно принять середину отрезка , т.е. .

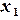Итерационный процесс состоит в последовательном уточнении . Каждый такой шаг называется итерацией. В результате итераций находятся последовательности приближенных значений корня , , …, . Если эта последовательность с ростом значения приближается к истинному значению корня, то итерационный процесс сходится. Итерационный процесс продолжаем до тех пор, пока значение функции после -й итерации не станет меньшим по модулю некоторого заданного малого числа , т.е. , и (или) по условию близости двух последних приближений: .