Для использования этого метода исходное нелинейное уравнение  необходимо привести к виду
необходимо привести к виду  .
.
В качестве 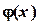 можно принять функцию
можно принять функцию  ,где M ‑ неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации
,где M ‑ неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации  . При этом для определения M условие сходимости записывается в следующем виде:
. При этом для определения M условие сходимости записывается в следующем виде:
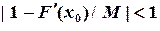 или
или 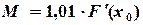 . (1.5)
. (1.5)
Если известно начальное приближение корня  , подставляя это значение в правую часть уравнения
, подставляя это значение в правую часть уравнения  , получаем новое приближение
, получаем новое приближение  .
.
Далее подставляя каждый раз новое значение корня в уравнение  , получаем последовательность значений:
, получаем последовательность значений:
 ,
,  ,...,
,...,  , k = 1,2,...,n.
, k = 1,2,...,n.
Итерационный процесс прекращается, если результаты двух последовательных итераций близки, т.е.  .
.
Геометрическая интерпретация метода простой итерации. Построим графики функций  и
и  . Корнем
. Корнем  уравнения
уравнения  является абсцисса пересечения кривой
является абсцисса пересечения кривой  с прямой
с прямой  (рис. 1.9). Взяв в качестве начальной точки
(рис. 1.9). Взяв в качестве начальной точки  , строим ломаную линию. Абсциссы вершин этой ломаной представляют собой последовательные приближения корня
, строим ломаную линию. Абсциссы вершин этой ломаной представляют собой последовательные приближения корня  . Из рисунка видно, что если
. Из рисунка видно, что если 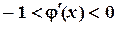 на отрезке
на отрезке  (рис. 1.9а), то последовательные приближения
(рис. 1.9а), то последовательные приближения  колеблются около корня. Если же производная
колеблются около корня. Если же производная  (рис. 1.9б), то последовательные приближения сходятся монотонно.
(рис. 1.9б), то последовательные приближения сходятся монотонно.

| 
|
| а)
| б)
|
| Рис. 1.9. Геометрическая интерпретация метода простой итерации.
|
Пример 1.4. Решить уравнение 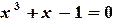 на отрезке
на отрезке  методом простой итерации c точностью
методом простой итерации c точностью  .
.
Решение. Из условия сходимости (1.5)  , при
, при  определяем
определяем  .Пусть
.Пусть  .
.
Подставляя каждый раз новое значение корня в уравнение
 ,
,
получаем последовательность значений:
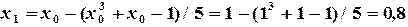


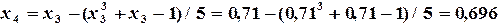
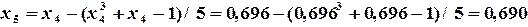
 , но
, но  , поэтому продолжаем вычисления.
, поэтому продолжаем вычисления.
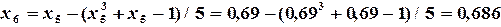
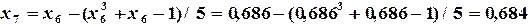
Теперь  и приближенным решением данного уравнения c точностью
и приближенным решением данного уравнения c точностью  является
является 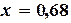 .
.
На рис.1.10 приведена программа решения данного уравнения методом простой итерации. В качестве исходных данных вводятся начальное приближение, точность вычисления и значение постоянной М.
|
| Исходные данные
| Результаты
|
| | A
| B
| C
| D
| E
|
|
| x0
| e
| M
| x
| F(x)
|
|
|
| 0,001
|
| 0,683335
| 0,002416
|
| Function F(x)
F = x ^ 3 + x - 1
End Function
Sub program3()
x = Cells(2, 1)
e = Cells(2, 2)
M = Cells(2, 3)
1 xk = x - F(x) / M
If Abs(xk - x) >= e Then x = xk: GoTo 1
Cells(2, 4) = xk
Cells(2, 5) = F(xk)
End Sub
|
| Рис. 1.10. Программа решения уравнения методом простой итерации на языке VBA.
|
Пример 1.4. Решить уравнение 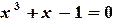 на отрезке
на отрезке  методом простой итерации c точностью
методом простой итерации c точностью  с помощью программы Excel.
с помощью программы Excel.
Порядок решения (рис. 1.11).
1) Ввести в ячейки A1:D1 заголовки столбцов.
2) В ячейку A2 – значение начального приближения 
3) В ячейку B3 – формулу функции =A2^3+A2-1
4) В ячейку C2 – значение M 5
5) В ячейку A3 – формулу первого приближения =A2-B3/$C$2
6) В ячейку D3 – погрешность =ABS(A3-A2)
7) Выделить ячейки A3:D3 и скопировать формулы в соседние ячейки расположенных ниже строк A4:D4, A5:D5, и т.д. при помощи маркера заполнения. Каждая новая строка содержит результаты очередного приближения.
8) В столбце A найти значение корня, соответствующее заданной точности.
Приближенное решение данного уравнения 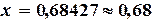 содержится в ячейке A9 (погрешность
содержится в ячейке A9 (погрешность  в ячейке D9).
в ячейке D9).
| | A
| B
| C
| D
|
|
| x
| f(x)
| M
| погрешность
|
|
|
|
|
|
|
|
| 0,8
|
|
| 0,2
|
|
| 0,7376
| 0,312
|
| 0,0624
|
|
| 0,70982
| 0,13889
|
| 0,02777881
|
|
| 0,69633
| 0,06746
|
| 0,01349237
|
|
| 0,68954
| 0,03396
|
| 0,00679209
|
|
| 0,68606
| 0,01738
|
| 0,0034769
|
|
| 0,68427
| 0,00897
|
| 0,00179463
|
| Рис.1.11. Решение уравнения методом простой итерации с помощью программы Excel.
|

 необходимо привести к виду
необходимо привести к виду  .
.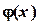 можно принять функцию
можно принять функцию  ,где M ‑ неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации
,где M ‑ неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации  . При этом для определения M условие сходимости записывается в следующем виде:
. При этом для определения M условие сходимости записывается в следующем виде: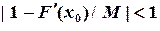 или
или 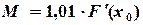 . (1.5)
. (1.5) , подставляя это значение в правую часть уравнения
, подставляя это значение в правую часть уравнения  .
. ,
,  ,...,
,...,  , k = 1,2,...,n.
, k = 1,2,...,n. .
. и
и  . Корнем
. Корнем  уравнения
уравнения  , строим ломаную линию. Абсциссы вершин этой ломаной представляют собой последовательные приближения корня
, строим ломаную линию. Абсциссы вершин этой ломаной представляют собой последовательные приближения корня 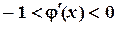 на отрезке
на отрезке  (рис. 1.9а), то последовательные приближения
(рис. 1.9а), то последовательные приближения  (рис. 1.9б), то последовательные приближения сходятся монотонно.
(рис. 1.9б), то последовательные приближения сходятся монотонно.

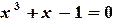 на отрезке
на отрезке  методом простой итерации c точностью
методом простой итерации c точностью  .
. , при
, при  определяем
определяем  .Пусть
.Пусть  .
. ,
,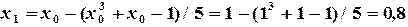


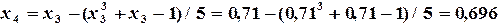
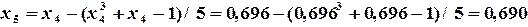
 , но
, но  , поэтому продолжаем вычисления.
, поэтому продолжаем вычисления.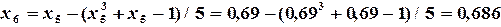
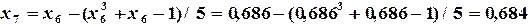
 и приближенным решением данного уравнения c точностью
и приближенным решением данного уравнения c точностью 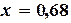 .
.
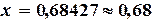 содержится в ячейке A9 (погрешность
содержится в ячейке A9 (погрешность  в ячейке D9).
в ячейке D9).


