Метод Гаусса.
Этот метод является одним из наиболее распространенных прямых методов решения систем линейных алгебраических уравнений. В основе метода Гаусса лежит идея последовательного исключения неизвестных. Рассмотрим систему из трех уравнений с тремя неизвестными:
Система уравнений (2.2) приводится к эквивалентной системе с треугольной матрицей:
Достигается это при помощи цепочки элементарных преобразований, при которых из каждой строки вычитаются некоторые кратные величины расположенных выше строк. Процесс приведения системы (2.2) к системе (2.3) называется прямым ходом, а нахождение неизвестных Прямой ход исключения: Исключаем В результате получаем следующую систему:
Из полученной системы (2.4) исключаем
Взяв из каждой системы (2.2), (2.4) и (2.5) первые уравнения, получим систему уравнений с треугольной матрицей. Обратный ход: Из уравнения (III²) находим Аналогичным путем методом Гаусса решаются системы Пример 2.1. Решить систему уравнений методом Гаусса:
Решение: Удалить члены с
2-я строка делится на
2-я строка умножается на
3-я строка делится на
Процедура обратного хода дает решение:
|

 (2.2)
(2.2) (2.3)
(2.3)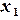 ,
,  ,
,  из системы (2.3) называется обратным ходом.
из системы (2.3) называется обратным ходом. и складываем со вторым, затем умножаем на
и складываем со вторым, затем умножаем на  и складываем с третьим.
и складываем с третьим. (2.4)
(2.4) и складывая со вторым уравнением, получим уравнение:
и складывая со вторым уравнением, получим уравнение: (2.5)
(2.5) . Из уравнения (II¢) находим
. Из уравнения (II¢) находим  . Из уравнения (I) находим
. Из уравнения (I) находим 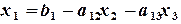 . Коэффициенты
. Коэффициенты  ,
,  называются ведущими элементами 1-го и 2-го шагов исключения неизвестных. Они должны быть отличны от нуля. Если они равны нулю, то, меняя местами строки, необходимо на их место вывести ненулевые элементы.
называются ведущими элементами 1-го и 2-го шагов исключения неизвестных. Они должны быть отличны от нуля. Если они равны нулю, то, меняя местами строки, необходимо на их место вывести ненулевые элементы. уравнений с
уравнений с 
 , а из 3-й - первую, умноженную на
, а из 3-й - первую, умноженную на  :
:
 :
:
 и вычитается из 3-й:
и вычитается из 3-й:
 :
:
 ;
;  ;
;



