Метод Ньютона решения систем нелинейных уравнений.
Основная идея метода Ньютона состоит в выделении из уравнений системы линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности систем линейных уравнений. Рассмотрим систему двух нелинейных уравнений с двумя неизвестными вида:
Пусть известно некоторое приближение
Для этого разложим функции
относительно неизвестных поправок Таким образом, решение системы уравнений по методу Ньютона состоит в построении итерационной последовательности:
где В методе Ньютона для обеспечения хорошей сходимости также важен правильный выбор начального приближения. Пример 3.2. Найти решение системы (3.8) методом Ньютона с точностью
Решение. Начальные приближения
и, используя (3.12), построим систему линейных уравнений относительно поправок
Подставляя начальные приближения
определяем поправки на первом шаге итерации
Далее начальное приближение уточняем по формулам (3.13)
Подставляя результаты первой итерации
определяем поправки на втором шаге итерации
Далее
Определяем погрешностьпо формуле
Таким образом, имеем решение: Программа, реализующая метод Ньютона для указанной задачи, представлена на рис. 3.2. Исходные данные – начальные приближения
Таблица 3.2. Исходные данные к программе решения системы нелинейных уравнений методом Ньютона
Пример 3.3. Найти решение системы (3.8) с помощью программы Excel.
|

 (3.10)
(3.10) ,
, 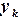 корня
корня 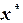 ,
,  . Тогда поправки
. Тогда поправки  ,
,  можно найти, решая систему:
можно найти, решая систему: (3.11)
(3.11) ,
, 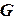 в ряд Тейлора по
в ряд Тейлора по 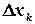 ,
,  . Сохранив только линейные по
. Сохранив только линейные по 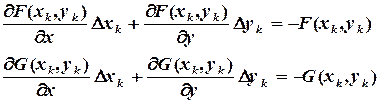 (3.12)
(3.12) (3.13)
(3.13) .
.
 ,
,  . Определим частные производные:
. Определим частные производные: ;
; 



 ,
,  ,
,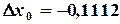 ,
, 
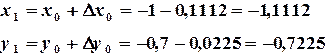
 ,
,  и решая систему линейных уравнений
и решая систему линейных уравнений ,
, ,
, 
 и
и  уточняем по формулам (3.13)
уточняем по формулам (3.13)
 :
:

 ,
,  .
. ,
,  , точность
, точность  и максимальное число итераций
и максимальное число итераций  (табл. 3.2).
(табл. 3.2).


