Пример моделирования
Рассмотримпримермоделированияприкоэффициенте усиления K =8 и постоянной времени апериодического звена T =4. Передаточная функция замкнутой системы при этом принимает следующий вид:
Корни характеристического уравнения
Процессы в такой системе будут носить колебательный характер с частотой f и периодом t собственных колебаний
Постоянная времени, с которой уменьшается амплитуда колебаний равна Исходя из полученных результатов расчета, задаем время интегрирования, равное В блоке интегрирования задаем начальное отклонение по X, равное 10. Соответственно в блоке XY_Graf задаем отклонения по X, также равное 10, а по оси Y больше в 1,4 раза и равное 15. Далее на рис. 5.2 показан результат моделирования в виде переходного процесса в функции времени, а на рис.3 показана фазовая траектория этого процесса. На рис.4 показан фазовый портрет системы, построенный по результатам моделирования четырех переходных процессов с соответствующими начальными отклонениями. По результатам моделирования можно сделать выводы: а) характер переходных процессов действительно носит колебательный характер, б) система управления устойчива, в) фазовый портрет состоит из траекторий в виде сужающихся эллипсов с устойчивым фокусом в точке равновесия.
Рис. 5.2.ПереходныйпроцессвсистемеприотклоненииX=10.
Рис. 5.3.ФазоваятраекторияприначальномотклоненииX=10
Содержание отчета Отчет о лабораторной работе должен содержать:
1. Цель работы. 2. Структурную схему системы автоматического управления и ее параметры. 3. Передаточныефункцииразомкнутыхсистем в соответствии с заданием. 4. Расчет передаточных функций замкнутых систем. 5. Расчет корней характеристического уравнения. 6. Расчеты всех постоянных времени и частот собственных колебаний. 7. Задание времени и шага интегрирования.
8. Задание параметров начального отклонения и исходных параметров блока XY_Graf. 9. Результаты моделирования в виде переходного процесса и в виде фазовой траектории. 10.Фазовый портрет системы автоматического управления. 11.Выводы о проделанной работе.
Контрольные вопросы 1. Что называется фазовым пространством?
2. Что показывает фазовая траектория движения системы?
3. Как на фазовом пространстве показывают начальные условия движения системы? 4. Что называется особой точкой фазовой траектории?
5. Где располагается особая точка на фазовой плоскости? 6. Что называется фазовой плоскостью? 7. Что называется фазовым портретом?
8. При каком значении демпфирования в колебательном звене фазовый портрет имеет устойчивый предельный цикл? 9. При каком значении демпфирования в колебательном звене фазовый портрет имеет устойчивый фокус? 10. При каком значении демпфирования в колебательном звене фазовый портрет имеет неустойчивый фокус? 11. При каком значении демпфирования в звене фазовый портрет имеет устойчивый узел? 12. При каком значении демпфирования в звене фазовый портрет имеет неустойчивый узел? 13. При каком значении демпфирования в колебательном звене фазовый портрет имеет вид седла?
|



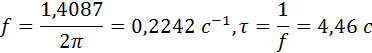

 а максимальный шаг выбираем меньше периода колебаний более чем в 40 раз и равным 0,1 с.
а максимальный шаг выбираем меньше периода колебаний более чем в 40 раз и равным 0,1 с.

 Рис. 5.4.Фазовыйпортретсистемыавтоматическогоуправления
Рис. 5.4.Фазовыйпортретсистемыавтоматическогоуправления


