Краткие теоретические сведения. Для наглядного представления сложной системы как совокупности элементов и связей между ними используются структурные схемы.
Для наглядного представления сложной системы как совокупности элементов и связей между ними используются структурные схемы. Структурной схемой называется схема САУ, изображенная в виде соединения ПФ составляющих ее звеньев. Структурная схема показывает строение автоматической системы, наличие внешних воздействий и точки их приложения, пути распространения воздействий и выходную величину. Динамическое или статическое звено изображается прямоугольником, в котором указывается ПФ звена или ее математическое выражение. Воздействия на систему и влияние звеньев друг на друга (сигналы) изображаются стрелками. В каждом звене воздействие передается только от входа звена к его выходу. На динамическое звено может воздействовать лишь одна входная величина, поэтому используются блоки суммирования и сравнения сигналов. Суммироваться и сравниваться могут лишь сигналы одной и той же физической природы. Структурная схема может быть составлена по уравнению системы в пространстве состояний или по дифференциальным уравнениям системы. При составлении структурной схемы удобно начинать с изображения задающего воздействия и располагать динамические звенья, составляющие прямую цепь системы, слева направо до регулируемой величины. Тогда основная обратная связь и местные обратные связи будут направлены справа налево. Различные способы преобразования структурных схем облегчают определение ПФ сложных САУ и дают возможность привести многоконтурную систему к эквивалентной ей одноконтурной схеме. Преобразование структурной схемы должно осуществляться на основании правил. Правила преобразования структурных схем можно найти в справочной литературе [1, 2], основные из них приведены в табл. 2.1. Таблица 2.1
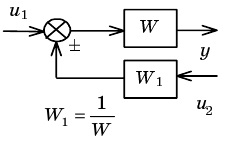
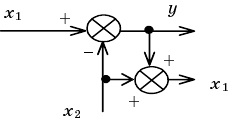
При выполнении преобразований следует каждое имеющееся в схеме типовое соединение заменить эквивалентным звеном. Затем можно выполнить перенос точек разветвления и сумматоров, чтобы в преобразованной схеме образовались новые типовые соединения звеньев. Эти соединения опять заменяются эквивалентными звенья ми, затем вновь может потребоваться перенос точек разветвления и сумматоров и т. д. Пример. Пусть необходимо получить эквивалентное представление для структуры, приведенной на рис. 2.1.
Рис. 2.1. Исходная структура САУ
Преобразование включает несколько этапов, показанных на рис.2.2-2.5.
Рис. 2.2. Перенос узла через сумматор
Рис. 2.3. Свертывание обратной связи и последовательного соединения
Рис. 2.4. Свертывание обратной связи и параллельного соединения
Рис. 2.5. Свертывание последовательного соединения Таким образом, первый способ преобразования структурных схем заключается в непосредственном использовании правил, приведенных в табл.2.1. Неудобство использования этого подхода заключается в том, что порядок применения формул здесь достаточно произволен, возможны ошибочные шаги, усложняющие поиск решения. Второй способ для получения ПФ многоконтурной системы заключается в использовании модели системы в виде сигнального графа. Сигнальный граф позволяет графически описать линейные связи между переменными, он состоит из узлов (вершин) и соединяющих их направленных ветвей. Ветвь соответствует блоку структурной схемы, она отражает зависимость между входной и выходной переменными. Сумма всех сигналов, входящих в узел, образует соответствующую этому узлу переменную. Последовательность ветвей между двумя узлами называется путем. Контуром называется замкнутый путь, который начинается и заканчивается в одном и том же узле, причем ни один узел не встречается на этом пути дважды. Коэффициент передачи контура - это произведение всех входящих в него дуг. Контуры называются не касающимися, если они не имеют общих узлов. Сигнальный граф однозначно соответствует структурной схеме. Пусть X(s) и Y(s) - входная и выходная переменные системы. Тогда для вычисления ПФ системы управления по ее графу можно воспользоваться формулой Мейсона:
где Определитель графа получается по формуле:
где -
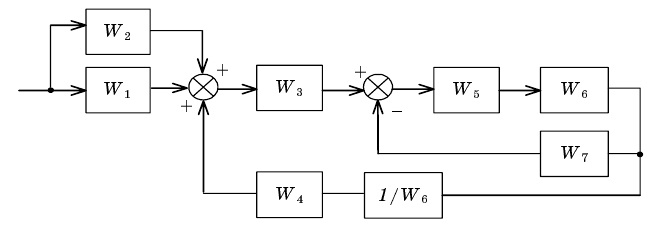
Дополнительный множитель для i -го пути равен определителю графа, в котором приравнены нулю коэффициенты передачи контуров, касающихся этого пути. Рассмотрим пример получения ПФ многоконтурной системы с использованием формулы Мейсона для структуры рис. 1, которой соответствует граф, показанный на рис. 2.6. От входа к выходу ведут два пути:
Рис. 2.6. Описание системы управления сигнальным графом
В графе есть два контура:
Контур
Контуры в этом примере касаются всех путей, поэтому дополнительные множители путей
Окончательно можно записать:
Таким образом, использование сигнальных графов и применение формулы Мейсона позволяет алгоритмизировать процесс упрощения структурной схемы.
|

























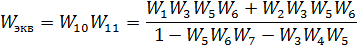

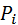 – i -й путь от входа к выходу; N - количество путей;
– i -й путь от входа к выходу; N - количество путей;  - определитель графа;
- определитель графа;  - дополнительный множитель для пути.
- дополнительный множитель для пути.
 сумма коэффициентов передачи всех отдельных контуров;
сумма коэффициентов передачи всех отдельных контуров; - сумма произведений всех возможных комбинаций из двух не касающихся контуров;
- сумма произведений всех возможных комбинаций из двух не касающихся контуров; - сумма произведений всех возможных комбинаций из трех некасающихся контуров.
- сумма произведений всех возможных комбинаций из трех некасающихся контуров.
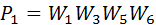


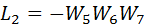
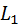 касается контура
касается контура  , поэтому определитель графа вычисляется по формуле:
, поэтому определитель графа вычисляется по формуле:





