Основы реперного формализма в декартовой системе координат.
Два вектора Найдем векторное произведение данных векторов:
Выражения в скобках получаются при вычислении определителей 2-го порядка, поэтому можно записать:
формула для нахождения векторного произведения векторов, заданных своими декартовыми координатами. Можем записать, что координаты вектора векторного произведения равны:
Примеры.
Основы реперного формализма в декартовой системе координат. Здесь рассмотрим понятия локального репера, векторного элемента длины и теорему Пифагора в декартовых координатах. Рассмотрим произвольную точку
Рис.1 Если ввести близкую к Из (1.1) следует, что
Это соотношение можно объяснить как разложение вектора
Рис.2 С другой стороны, (1.2) можно получить дифференцированием (1.1), считая Из (1.1) следует, что
Квадрат расстояния между близкими точками определяется теоремой Пифагора
Это соотношение можно получить из (1.2), используя таблицу скалярных произведений декартова репера:
(1.5)
Следовательно, таблица скалярных произведений (1.5) эквивалентна теореме Пифагора (1.4), и позволяет определить важный геометрический объект, называемый метрическим тензором. Введем индексные обозначения:
(1.7)
Кроме того, определим символ Кронекера:
Тогда таблица скалярных произведений декартова репера (1.5) записывается в форме:
Таким образом, метрическим тензором называется тензор второго ранга, компоненты которого в декартовой системе координат совпадают с символом Кронекера.
|

 и
и 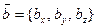 заданы своими декартовыми координатами. Разложим их по ортам
заданы своими декартовыми координатами. Разложим их по ортам  :
:  ,
,  .
.



 (воспользуемся таблицей векторного умножения ортов и сгруппируем) = =
(воспользуемся таблицей векторного умножения ортов и сгруппируем) = = 
 .
. –разложение по первой строке определителя 3-го порядка:
–разложение по первой строке определителя 3-го порядка: – (4)
– (4) .
. , положение которой в пространстве определяется его радиус-вектором:
, положение которой в пространстве определяется его радиус-вектором: . (1.1)
. (1.1)
 , то разность радиус-векторов положения этих двух точек определяет бесконечно малый вектор, называемый векторным элементом длины.
, то разность радиус-векторов положения этих двух точек определяет бесконечно малый вектор, называемый векторным элементом длины. . (1.2)
. (1.2) по декартовому базису из единичных векторов
по декартовому базису из единичных векторов  .
.
 . (1.3)
. (1.3) . (1.4)
. (1.4)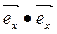 =
=  =
=  = 1
= 1 =
=  =
=  = 0
= 0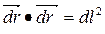 . (1.6)
. (1.6) ;
; .
.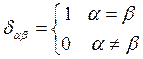 , где
, где  (1.8)
(1.8) (1.9)
(1.9)


