Электростатическое поле распределения зарядов с симметрией плоскости
Симметрия плоскости соответствует распределению зарядов внутри неограниченной плиты толщины 2 L с
Середина плиты совмещена с плоскостью xy. Распределение зарядов не зависит от xу, т.е. имеет симметрию плоскости. Пусть
Для того, чтобы иметь дело с конечными значениями зарядов - в теореме Гаусса, рассмотрим область
а) Найдем Через точки
Рис.9
Параллелепипед имеет шесть граней. Ненулевой вклад в уравнение, выражающее теорему Гаусса дадут только элементы
а четыре элемента от боковых граней вида
перпендикулярны вектору напряженности и поэтому поверхностные интегралы по боковым граням обращаются в нуль. Таким образом, теорема Гаусса выражается соотношением:
Вычислим количество заряда, которое имеет рассматриваемый параллелепипед:
Подставим (**) в (*) и получим
б) Аналогичными рассуждениями находим напряженность поля
в) Согласно полученным результатам и (8.2) составим дифференциальные уравнения для определения потенциалов внутри Учтем, что
Следовательно, внутри плиты:
Положим, что потенциал
Условия «сшивания» внешнего и внутреннего решений при
В нижнем полупространстве имеют место соотношения;
Условия «сшивания» внешнего и внутреннего решений имеют вид:
Объединим полученные формулы следующим образом:
Эти формулы описывают значения потенциалов внутри и вне плиты при любых значениях z.
|

 (8.1)
(8.1)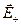 - напряженность при z > 0, а
- напряженность при z > 0, а  - напряженность при z < 0. Тогда симметрия
- напряженность при z < 0. Тогда симметрия  приводит к тому, что
приводит к тому, что (8.2)
(8.2) (8.3)
(8.3) трехмерного пространства, ограниченную плоскостями
трехмерного пространства, ограниченную плоскостями
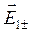 внутри плиты.
внутри плиты. и
и  , отстоящие друг от друга на расстоянии
, отстоящие друг от друга на расстоянии  проведем плоскости, параллельные ху и применим теорему Гаусса для полученного объема в форме параллелепипеда (рис.9).
проведем плоскости, параллельные ху и применим теорему Гаусса для полученного объема в форме параллелепипеда (рис.9).
 (8.4)
(8.4) (8.5)
(8.5) (*)
(*) (**)
(**) (8.6)
(8.6) (8.7)
(8.7) вне плиты:
вне плиты: (8.8)
(8.8) (8.9)
(8.9)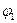 и
и  вне плиты.
вне плиты. при z > 0 и
при z > 0 и  при z < 0. Тогда формулы (8.7) можно объединить:
при z < 0. Тогда формулы (8.7) можно объединить: (8.10)
(8.10) (*)
(*) (**)
(**)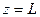 , приводят к тому, что
, приводят к тому, что (***)
(***) (8.11)
(8.11) (****)
(****) (8.12)
(8.12) (8.13)
(8.13)


