Закон Био-Савара. Распределения объемных плотностей тока, типа полученных выше формул, позволяют сводить к квадратурам задачу об определении компонент вектора напряженности
Распределения объемных плотностей тока, типа полученных выше формул, позволяют сводить к квадратурам задачу об определении компонент вектора напряженности магнитного поля на основе закона Био-Савара:
Найти напряженность магнитного поля в вакууме, создаваемое током, силы I, текущим по прямому тонкому проводу бесконечной длины. Решение:Ось z цилиндрической системы координат совместим с проводом.
Рис.12
Используя нормировочное условие
и очевидное соотношение
найдем, что
Рассмотрим точку Р с координатами Предельный переход
Рис.13
Радиус-вектор
Точка наблюдения Р определяется радиус-вектором:
Отсюда следует, что
Таблица векторных произведений базисных ортов цилиндрической системы координат имеет вид:
Следовательно,
Подставим все полученные результаты в формулу (10.1) и получаем
Учтем, что
Окончательно, имеем
Задача решена.
|

 (10.1)
(10.1)
 (10.2)
(10.2)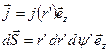 (10.3)
(10.3) (10.4)
(10.4) . Вычислим
. Вычислим  , создаваемое участком
, создаваемое участком  .
. даст поле бесконечного провода, которое обладает осевой симметрией относительно вращений (вокруг оси z) и трансляционной симметрией для сдвигов по оси z.
даст поле бесконечного провода, которое обладает осевой симметрией относительно вращений (вокруг оси z) и трансляционной симметрией для сдвигов по оси z.

 положения элемента объема
положения элемента объема  в интеграле (10.1) пробегает все трехмерное пространство:
в интеграле (10.1) пробегает все трехмерное пространство: (10.5)
(10.5)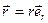 (10.6)
(10.6) (10.7)
(10.7) (10.8)
(10.8) (10.9)
(10.9) (10.10)
(10.10) (*)
(*)


 (10.11)
(10.11) (10.12)
(10.12)


