Определение напряженности и потенциала электростатического поля для сферически симметричного распределения зарядов.
Пусть имеется замкнутая поверхность почти произвольной формы, но такая, что лучи, проводимые из некоторой точки, находящейся внутри, протыкают ее только один раз. Обозначим через Q количество заряда, находящегося внутри S.
Рис.6
Тогда электростатическая теорема Гаусса выражается интегральным соотношением:
Пусть распределение объемной плотности заряда сферически-симметрично, т.е. в сферических координатах
Потенциал электростатического поля определяется из уравнения Пуассона:
Из-за сферической симметричности правой части такую же симметрию должна иметь левая часть уравнения и в лапласиане члены с угловыми переменными должны исчезнуть. Тогда решение (6.3) может быть только сферически-симметричным:
В определение напряженности электростатического поля подставим формулу для градиента в сферической системе координат
и получим вектор напряженности сферически-симметричного электростатического поля:
Решим следующую задачу. Имеется шар радиуса, заряженный с объемной плотностью, имеющей сферическую симметрию
Найти напряженность Решение. А) Найдем
Рис.7 Теорема Гаусса для гласит, что
В правой части стоит
С другой стороны, вычисляя скалярное произведение в подынтегральном выражении (6.8) согласно (6.6) и (4.11) имеем
Подставляя промежуточные результаты (*,**) в (6.7) получаем значение компоненты вектора напряженности внутри сферы
Б) Найдем
Через точку
Учитывая (*), отсюда получаем, что
В) Найдем потенциалы
Решение этого уравнения получается методом разделения переменных:
Постоянная интегрирования B оказывается равной нулю, если положить, что
Для потенциала
Решение этого уравнения имеет вид:
Постоянную интегрирования D найдем из условия «сшивания» внешнего и внутреннего решений на границе
Отсюда следует, что
Решение задачи имеет вид:
|


 , (6.1)
, (6.1) - напряженность электростатического поля.
- напряженность электростатического поля. . (6.2)
. (6.2) . (6.3)
. (6.3) . (6.4)
. (6.4) , (6.5)
, (6.5) . (6.6)
. (6.6) - const. (6.7)
- const. (6.7) электростатического поля вне и внутри шара.
электростатического поля вне и внутри шара. внутри шара радиуса R. Через произвольную точку P, находящуюся внутри сферы
внутри шара радиуса R. Через произвольную точку P, находящуюся внутри сферы  радиуса R проведем сферу
радиуса R проведем сферу  радиуса r<R.
радиуса r<R.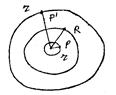
 . (6.8)
. (6.8) – количество заряда, находящееся внутри сферы
– количество заряда, находящееся внутри сферы  . (*)
. (*)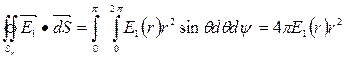 . (**)
. (**)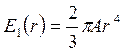 . (6.9)
. (6.9) вне сферы
вне сферы  . (*)
. (*) , находящуюся вне сферы
, находящуюся вне сферы  . (**)
. (**) . (6.10)
. (6.10) внутри
внутри  вне
вне  . (6.11)
. (6.11) . (6.12)
. (6.12)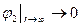 . (6.13)
. (6.13) . (6.14)
. (6.14) . (6.15)
. (6.15)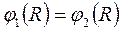 . (6.16)
. (6.16)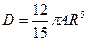 . (6.17)
. (6.17) ;
; ;
;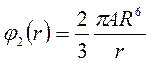 ;
; (6.18)
(6.18)


