Метрический тензор и коэффициенты Ламе.
Квадрат расстояния между близкими точками определяется теоремой Пифагора. Для формулировки этой теоремы в криволинейной системе координат заметим, что компоненты введенного в § 1 метрического тензора здесь определяются таблицей скалярных произведений натурального репера
Используя формулы (2.10) и (2.12) легко установить, что в сферической и цилиндрической системах координат имеем следующую таблицу:
Ниже r – цилиндрический радиус:
Уравнение (1.6), которое вместе с соотношением (1.4) определяет формулировку теоремы Пифагора в декартовых координатах, записано в векторной форме, и следовательно, остается справедливым в любой системе координат. Подставляя (2.7) и (3.1) в (1.6), получаем формулировку теоремы Пифагора в произвольной криволинейной системе координат:
Соответственно, в сферической и цилиндрической системах координат имеем
Скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними. Отсюда следует, что благодаря касательности векторов натурального репера к координатным линиям, последние будут взаимно-ортогональны в каждой точке, если недиагональные компоненты метрического тензора равны нулю
Такие системы координат называются криволинейными ортогональными, в дальнейшем всегда будем пользоваться ими. Из формул (3.2) и (3.4) видно, что координатные линии сферической и цилиндрической систем координат взаимно-ортогональны во всех точках пространства. В криволинейной ортогональной системе координат теорема Пифагора согласно (3.9) принимает вид:
Введем величины
которые называются коэффициентами Ламе. Если определить элементарные длины
то (3.10) принимает тот же вид, что теорема Пифагора в декартовой системе координат:
Из определения (3.11) следует, что коэффициенты Ламе совпадают с «длинами» соответствующих векторов натурального репера:
В формулы преобразования координат Если сделать нормировку векторов натурального репера, то получаются векторы ортонормированного репера, присоединенного к криволинейной ортогональной системе координат:
Для сферических и цилиндрических координат на основании (2.10) и (2.12) коэффициенты Ламе и формулы перехода к ортонормированному реперу имеют вид:
|

 . (3.1)
. (3.1) ,
, 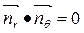 ,
, ,
,  , (3.2)
, (3.2) ,
,  ,
, . (3.3)
. (3.3) ,
,  , (3.4)
, (3.4) ,
, 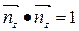 ,
, . (3.5)
. (3.5) . (3.6)
. (3.6)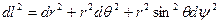 , (3.7)
, (3.7)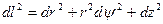 , (3.8)
, (3.8) ,
, 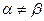 . (3.9)
. (3.9) . (3.10)
. (3.10)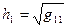 ,
,  ,
,  , (3.11)
, (3.11) ,
,  ,
, 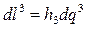 , (3.12)
, (3.12) . (3.13)
. (3.13) ,
,  ,
,  . (3.14)
. (3.14) входят нелинейным образом. Поэтому они должны быть безразмерными величинами. Тогда из (3.12) видно, что коэффициенты Ламе имеют размерность длины.
входят нелинейным образом. Поэтому они должны быть безразмерными величинами. Тогда из (3.12) видно, что коэффициенты Ламе имеют размерность длины.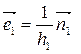 ,
,  ,
,  . (3.15)
. (3.15)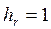 ,
,  ,
,  ,
,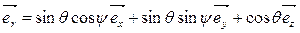 , (3.16)
, (3.16) ,
, , (3.17)
, (3.17) ,
,  , (3.18)
, (3.18) ,
, , (3.19)
, (3.19) .
.


