Применение дельта-функции Дирака и ступенчатой функции для описания распределения объемной плотности тока
Объемные плотности заряда и тока для случаев типа распределения зарядов по поверхности, линии и других ограниченных областей записываются в виде скалярной и векторной функций, определенных во всем трехмерном пространстве. Свойства дельта-функции и ступенчатой функции и их применение даны в задачнике [1]. Желательно прорешать задачи 80,81,88 и проработать приложения о свойствах указанных обобщенных функций в [1]. Разберем подробно решения двух задач из [1]. 149 г): В плоскости ху по бесконечно тонкому кольцу радиуса R течет линейный ток J, образуя правовинтовую систему с осью z, которая проходит через центр кольца. Используя дельта-функцию Дирака определить распределение объемной плотности тока
Рис.10
Решение: Некоторое значение азимутального угла
Плотность тока отлична от нуля при следующих значениях цилиндрических координат:
Поэтому вектор объемной плотности тока нужно искать в виде:
А - нормировочный множитель.
получаем
Задача решена. 149 д): Найти Решение: Известно, что
Поэтому сначала найдем распределение объемной плотности заряда
Следовательно,
Нормировочный множитель А найдем из условия:
Вычислив объемный интеграл в этой формуле по всему трехмерному пространству получим, что
Найдем результат векторного произведения (9.7) в сферической системе координат.
Рис.11
Пусть
тогда
Легко видеть, что
В силу взаимной ортогональности базисных ортов сферической системы координат для них имеет место следующая таблица векторных произведений:
Следовательно,
Задача решена.
|

 .
.
 определяет плоскость
определяет плоскость  . Согласно определению понятия силы тока имеем нормировочное условие для искомой объемной плотности тока:
. Согласно определению понятия силы тока имеем нормировочное условие для искомой объемной плотности тока: (9.1)
(9.1) (9.2)
(9.2) (9.3)
(9.3) В силу того, что
В силу того, что (9.4)
(9.4) (9.5)
(9.5) , если равномерно заряженная с поверхностной плотностью
, если равномерно заряженная с поверхностной плотностью  поверхность кругового конуса с вершиной в начале координат вращается вокруг своего диаметра с угловой скоростью
поверхность кругового конуса с вершиной в начале координат вращается вокруг своего диаметра с угловой скоростью  , направленной вдоль оси z.
, направленной вдоль оси z. (9.6)
(9.6) (9.7)
(9.7) . Очевидно, что в сферической системе координат
. Очевидно, что в сферической системе координат (9.8)
(9.8) (9.9)
(9.9) (9.10)
(9.10) (9.11)
(9.11)
 (*)
(*) (**)
(**)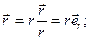 (9.12)
(9.12) (9.13)
(9.13) (9.14)
(9.14) (9.15)
(9.15) (9.16)
(9.16)


