Теория потенциала
11.1 Метод частного интегрирования
11.1.1. Представление неопределенного интеграла как обратного оператора для дифференцирования функции
Любой известной функции
Значение производной является новой функцией, которую обозначим следующим образом
Можно сформулировать обратную задачу: по заданной функции
Введем оператор интеграла как обратное к дифференциалу действие на функцию
Можно написать символическое уравнение для взаимно обратных и перестановочных операторов интегрирования и дифференцирования
Умножая (11.3) на оператор интегрирования получаем соотношение
Последнее слагаемое, равное произвольной постоянной, при дифференцировании этого соотношения исчезает. Оно известно как константа интегрирования. Подстановка (11.6) превращает (11.3) в тождество и поэтому она является общим решением дифференциального уравнения (11.3). Здесь «дифференциальным» называем уравнение, содержащее символы дифференцирования неизвестной функции. Покажем, что (11.6) удовлетворяет уравнению (11.2)
Отсюда следует, что оператор полной производной и неопределенный интеграл от функции взаимно обратны
Символические вычисления позволяет доказать перестановочность этих двух операций
Литература 1. Алексеев А.Н. Сборник задач по классической электродинамике. М.: Наука, 1977. §1. Основы реперкого формализма в декартовой системе координат §2. Натуральный репер, присоединенный к криволинейной системе координат §3. Метрический тензор и коэффициенты Ламе §4. Конструирование основных типов векторных интегралов §5. Два основных свойства криволинейных, поверхностных и объемных интегралов §6. Определение напряженности и потенциала электростатического поля для сферически симметричного распределения зарядов §7. Цилиндрически-симметричное распределение зарядов §8. Электростатическое поле распределения зарядов с симметрией плоскости §9. Применение дельта-функции Дирака и ступенчатой функции для описания распределения объемной плотности тока §10. Закон Био-Савара
|

 от одного переменного можно сопоставить её производную, равную пределу
от одного переменного можно сопоставить её производную, равную пределу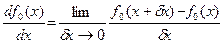 . (11.1)
. (11.1) (11.2)
(11.2) найти такую функцию
найти такую функцию 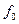 , которая удовлетворяет уравнению (11.2). Последняя функция в математическом анализе называется первообразной исходной функции
, которая удовлетворяет уравнению (11.2). Последняя функция в математическом анализе называется первообразной исходной функции  (11.3)
(11.3)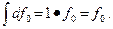 (11.4)
(11.4)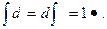 (11.5)
(11.5) (11.6)
(11.6) (11.7)
(11.7) (11.8)
(11.8) (11.9)
(11.9)


