Конструирование основных типов векторных интегралов.
Криволинейные интегралы скалярного и векторного характера строятся при использовании векторного элемента длины (1.2), который в криволинейной ортогональной системе согласно (2.7) имеют вид:
В сферических и цилиндрических координатах имеем
Криволинейный интеграл скалярного типа получается, если в качестве подынтегрального выражения взять скалярное умножение вектор-функции
А если вместо скалярного умножения составить векторное произведение, то получится интеграл векторного типа:
Поверхностные интегралы двух типов конструируются аналогичным образом. Скалярный интеграл получится по аналогии с (4.4), где роль
Если здесь скалярное произведение заменить векторным, то получится векторный интеграл. Для вычисления таких интегралов нам понадобятся формулы для векторных элементов длины и поверхности и элемента объема в криволинейных ортогональных системах координат. Перепишем (4.1), вводя туда элементарные длины (3.12):
Сравним это выражение с (1.2) и видим, что (4.8) получается из (1.2) заменой
Эту же замену произведем в (4.6) и получим общую формулу для векторного элемента поверхности:
В сферических и цилиндрических координатах эта формула принимает вид:
Произведя такую же замену в элементе объема, записанном в декартовой системе координат
получим элемент объема в криволинейной ортогональной системе координат:
В сферической и цилиндрической системах:
|

 . (4.1)
. (4.1) ; (4.2)
; (4.2) . (4.3)
. (4.3) на векторный элемент длины:
на векторный элемент длины: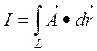 . (4.4)
. (4.4) . (4.5)
. (4.5) играет векторный элемент поверхности
играет векторный элемент поверхности  , который в декартовой системе координат имеет вид:
, который в декартовой системе координат имеет вид:
 ; (4.6)
; (4.6) . (4.7)
. (4.7) . (4.8)
. (4.8)
 ;
; (4.9)
(4.9) .
. . (4.10)
. (4.10)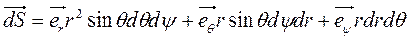 ; (4.11)
; (4.11) . (4.12)
. (4.12) , (4.13)
, (4.13) . (4.14)
. (4.14) ; (4.15)
; (4.15)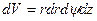 . (4.16)
. (4.16)


