
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Поняття публічної обіцянки винагороди
Дата добавления: 2015-10-15; просмотров: 807
|
|
(блок-схема, программа)
задачи из геометрии
1) Дана длина ребра куба. Найти объем куба и площадь его боковой поверхности.
2) Даны длины сторон трапеции. Найти периметр трапеции.
3) Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.
4) Определить периметр правильного n-угольника, описанного около окружности радиуса R.
5) Дана сторона равностороннего треугольника. Найти площадь этого треугольника.
6) Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет и радиус вписанной окружности.
7) Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
8) Найти площадь кольца, внутренний радиус которого равен 20, а внешний – заданному числу R.
9) Треугольник задан величинами своих углов и радиусом описанной окружности. Найти стороны треугольника.
10) Треугольник задан длинами сторон. Найти: а) длины высот; б) длины медиан; в) длины биссектрис; г) радиусы вписанной и описанной окружностей.
11) Треугольник задан координатами своих вершин. Найти: периметр и площадь треугольника.
12) Найти площадь равнобочной трапеции с основаниями a и b и углом α при большем основании а.
13) Найти площадь сектора, радиус которого равен 13.7, а дуга содержит заданное число радиан φ.
задачи из математики
1) Найти сумму членов арифметической прогрессии a, a+d,…a+(n-1)d по данным значениям a,d,n.
2) Даны действительные положительные числа a, b, c. По трем сторонам с длинами a, b, с можно построить треугольник. Найти углы треугольника.
3) Определите число, полученное выписыванием в обратном порядке цифр заданного целого трехзначного числа x.
4) Дано натуральное число n, состоящее из шести цифр. Определите число сотен и тысяч в нем.
5) Дано значение угла в градусах. Определите смежный к нему угол в радианах.
6) Для произвольных чисел a, b, c определите, имеет ли уравнение ax2 + bx + c = 0 хотя бы одно вещественное решение.
7) Даны три положительных числа a, b, c. Определите, можно ли построить треугольник с такими длинами сторон.
8) Определите, есть ли среди цифр некоторого трехзначного числа повторяющиеся.
9) Определите, равна ли сумма крайних цифр некоторого четырехзначного числа сумме его средних цифр.
задачи из физики
1) Даны значения средней скорости и время движения автомобиля. Определите пройденный автомобилем путь за заданное время.
2) Даны значения V1, V2 и S. Написать алгоритм для решения следующей задачи: скорость первого автомобиля V1 км/ч, второго – V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся в разные стороны?
3) Даны значения V1, V2 и S. Написать алгоритм для решения следующей задачи: скорость первого автомобиля V1 км/ч, второго – V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся навстречу друг другу?
4) Определите идеальный вес человека по его росту, при условии, что идеальный вес (кг)=рост(см)—100.
Написать оператор присваивания, в результате которого некоторая логическая переменная принимает значение true, если выполняется указанное условие, и значение false - в противном случае:
| числа x,y,z равны между собой; |
| из чисел x,y,z только два равны между собой; |
| целые числа x,y имеют одинаковую четность; |
| цифра 7 входит в запись трехзначного целого числа k хотя бы один раз; |
| точка A(x,y) попадает внутрь круга радиуса R. |
Записать выражения, истинные при выполнении указанного условия и ложные в противном случае:
| х Î [0,1); |
| х Ï [0,1); |
| х Î отрезку [2,5] или отрезку [-1,1]; |
| х Ï отрезкам [2,5] и [-1,1]; |
| каждое из чисел x,y,z положительно; |
| x=min(x,y,z). |
| значение A не принадлежит интервалу (0,3) |
| значение A принадлежит отрезку [-2,0] |
| значение A принадлежит одному из отрезков: [-5,-4],[0,2],[3,2;7] |
| точка A с координатами (X,Y) лежит внутри круга с центром в начале координат и радиусом 2,3 |
| точка A с координатами (X,Y) лежит на границе или вне единичного круга с центром в начале координат |
Каков будет результат программы?
| var a,b : integer; begin write('Введите три числа '); read(a,b,a); write(a,b,a) end. | |
| var x:real; t:boolean; begin read(x); t:=x<round(x); read(x); t:=t and (x<trunc(x)) write(t) end. |
Найти ошибки в следующих программах:
| program A; const d=5; begin d:=sqr(5); writeln('d*d=',d); end. | |
| program B; const k=true; var x:real; begin read(x); writeln(ord(x)=k); end. | |
| program C; const p=3.14159; var a,b:integer; begin read(a); d:=odd(p*0) and b>a; writeln(d); end. | |
| program D; var a,b:integer; x:real; begin read('a=',a,'b=',b); x:=a+a/b; b:=x mod a; write('a=',a:5:2,'b=',b:5:2); writeln('x=',x:5) end. |
Расчет оптимального размера заказа
Наиболее распространенной моделью прикладной теории логистики является модель оптимального или экономичного размера заказа EOQ (Economic Order Quantity) [2, 5, 11 и др]. В качестве критерия оптимизации принимается минимум общих затрат CΣ, включающих затраты на выполнение заказов Сз и затраты на хранение запаса на складе Сx в течение определенного периода времени (год, квартал и т.п.)
 (6.1)
(6.1)
где: С0 -затраты на выполнение одного заказа, руб;
А - потребность в заказываемом продукте в течение данного периода, шт.;
Сn - цена единицы продукции, хранимой на складе, руб.;
i - доля от цены Сn, приходящейся на затраты по хранению;
S - искомая величина заказа, шт.
На рис.6.1 представлены составляющие затрат C3 и Cx и суммарные затраты CΣ в зависимости от размера заказа.
Из рис.6.1 видно, что затраты на выполнение заказов с увеличением размера заказа уменьшаются, подчиняясь гиперболической зависимости (кривая1); затраты на хранение партии поставки возрастают прямо пропорционально размеру заказа (линия 2); кривая общих затрат (кривая 3), имеет вогнутый характер, что говорит о наличии минимума, соответствующего оптимальной партии S0.
Значение оптимума S0 совпадает с точкой пересечения зависимостей C3 и Cx. Это объясняется тем, что абсцисса точки пересечения S находится из решения уравнения
 (6.2)
(6.2)
 |
Рис. 6.1 Зависимость затрат от размера заказа: 1 – затраты на выполнение заказа; 2 – затраты на хранение; 3 – суммарные затраты.
то есть
 (6.3)
(6.3)
При других зависимостях C3 = f(S) и Cx = f(S) указанного, совпадение может не наблюдаться и в этом случае необходимо применить процедуру оптимизации. Так, для функции (6.1) находим
 (6.4)
(6.4)
Решая уравнение (6.4), приходим к формуле (6.3) для определения EOQ.
Зная S0, нетрудно определить количество заказов
N=A / S0 , (6.5)
минимальные суммарные затраты за рассматриваемый период
 (6.6)
(6.6)
время между заказами
T3=ДpS0 / A=Дp / N, (6.7)
где Др – продолжительность рассматриваемого периода.
Если речь идет о количестве рабочих дней в году, то Дp=260 дней, если о количестве недель, то Дp=52 недели.
Формула (6.3) встречается в различных источниках под следующими названиями: Уилсона (наиболее распространенная), Вильсона, Харриса, Кампа.
Формула (6.3) получена при большом количестве допущений:
· затраты на выполнение заказа Co, цена поставляемой продукции Сп и затраты на хранение единицы продукции в течение рассматриваемого периода постоянны;
· период между заказами (поставками) постоянный, т.е. Тз = const.;
· заказ So выполняется полностью, мгновенно;
· интенсивность спроса  - постоянна;
- постоянна;
· емкость склада не ограничена;
· рассматриваются только текущие (регулярные) запасы, другие виды запасов (страховые, подготовительные, сезонные, транзитные и т.д.) не учитываются.
Анализ ряда работ показал, что трактовка затрат Сo, связанных с заказом, носит дискуссионный характер. Так, в большинстве работ Сo включает транспортно-заготовительные затраты: от расходов на заключение договора и поиска поставщиков до оплаты услуг по доставке. Например, в работе [11] затраты на поставку единицы заказываемого продукта включают следующие элементы:
· стоимость транспортировки заказа;
· затраты на разработку условий поставки;
· стоимость контроля выполнения заказа;
· затраты на выпуск каталогов;
· стоимость форм документов.
В других работах, например [23], транспортные затраты не входят в C0 и представлены в виде дополнительных слагаемых в формуле (6.1): собственно затрат на транспортировку и затрат, связанных с запасами на время в пути.
Еще один вариант учета транспортных затрат состоит в том, что они учитываются в стоимости единицы продукции Cn, поступивший на склад. Если покупатель сам оплачивает транспортные расходы и несет полную ответственность за груз в пути, то это приводит к тому, что при оценки стоимости товаров, хранящихся на складе в качестве запасов, к их закупочной цене следует прибавить транспортные расходы [2, стр.246].
В табл.6.1 приведены результаты расчетов оптимальной партии заказа: количество заказов в год и периодичность заказа при Дp=260 дней. Из табл.6.1 видно, что формула (3) охватывает широкий диапазон величины заказов в течение расчетного периода; при этом составляющая i, связанная с оценкой затрат на хранение в основном колеблется в довольно узком диапазоне 0,2-0,25.
О распространении формулы (6.3) говорит такой факт, что фирма «Вольво» снабжает своих агентов и дилеров специальной счетной линейкой, разработанной на основе формулы Уилсона [22]. Однако проведенные исследования показали, что даже с соблюдением всех ограничений, допущения, принятые при выводе формулы Уилсона, требуют уточнения, в частности, затраты на хранение.
В модели (6.1) предполагается, что оплата за хранение единицы продукции пропорциональна ее цене, а среднее количество находящейся на хранении продукции при постоянной интенсивности спроса на данный период времени равно
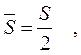 (6.8)
(6.8)
Таблица 6.1.
Исходные данные и оптимальные размеры заказа, рассчитанные по формуле Уилсона
| Исходные данные | S0, шт. | Кол-во заказов N | Периодичность заказа, Т3, дн. | Источник | |||
| C0 | A | Cn | i* | ||||
| 0,20 | Аникин Б.А. и др. [11] | ||||||
| 0,10 | Гаджинский А.М.,[5] | ||||||
| 0,1 | Неруш Ю.М. [17] | ||||||
| 60,8 | 29,3 | 0,22 | Сергеев В.И. [23] | ||||
| 0,2 | Бауэрсокс Д., Клосс Д. [2] | ||||||
| 45** | 0,25 | Линдерс М., Фарон Х. [10] | |||||
| Shapiro S.F. | |||||||
| 0,2 | Джонсон Д. и др. [7] | ||||||
| Примечание: *)-доля от годовой стоимости запаса на хранение; **)- в стоимость хранения включены затраты на транспортировку; |
Из рис.6.2 виден принцип получения зависимости  . Так, если бы за время Т был произведен один заказ, равный потребности в заказываемом продукте А, то в среднем на хранении находилось бы А/2 продукции. Если два заказа с интервалом T/2, то среднее количество хранимой продукции было бы А/4 и т.д.
. Так, если бы за время Т был произведен один заказ, равный потребности в заказываемом продукте А, то в среднем на хранении находилось бы А/2 продукции. Если два заказа с интервалом T/2, то среднее количество хранимой продукции было бы А/4 и т.д.

Рис.6.2 определение средней величины запаса на складе:
а) – максимальный запас А; б)-максимальный запас А/2
Однако, практика аренды складских помещений, а также расчеты затрат на хранение на складах ряда фирм, говорят о том, что как правило учитывается не средний размер партии, а площадь (или объем) склада, которая требуется для всей поступившей партии
Сx = akS, (6.9)
где: а- затраты на хранение единицы продукции с учетом занимаемой площади (объема) склада, руб.\м2 (руб.\м3);
к- коэффициент, учитывающий пространственные габариты единицы продукции, м2\шт. (м3\шт.).
С учетом (6.9) расчетная формула для оптимальной величины заказа запишется в виде
 , (6.10)
, (6.10)
Теперь, когда становится ясным, что оплата за хранение продукции может быть связана не только с величиной  , предлагается ввести более гибкую зависимость вида
, предлагается ввести более гибкую зависимость вида
Cx = βCn iS, (6.11)
где: β - коэффициент, отражающий связь между долей от стоимости объема заказа и установленной арендной платой. Коэффициент β может изменяться в широких пределах.
При подстановке (6.11) в формулу (6.1) после преобразований находим
 , (6.12)
, (6.12)
При β = 0,5 приходим к зависимости (3).
Вторым не мене важным условием, которое необходимо учитывать при расчете EOQ, являются скидки. Известно, что при покупке партии товара большинство фирм дает скидки, величина которых зависит от размера партии S.
Наиболее часто в работах по управлению запасами приводится дискретные зависимости, отражающие изменение цены единицы продукции Cnj от размера партии Si, рис.6.3. Здесь возможны различные ситуации. Первая, когда цена меняется, а затраты на хранение остаются такими же, т.е. не зависят от изменения цены. Вторая, когда вместе с изменением цены пропорционально изменяются затраты на хранение. Третья, наиболее общая, ситуация, при которой между изменениями цены и изменяющимися затратами на хранение не наблюдается однозначной зависимости. Для примера в табл.6.2 приведены скидки на цены и затраты на хранение в зависимости от размера партии [17].
Аналитическая зависимость общих издержек, связанных с запасами, записывается в виде системы уравнений для каждой j-й цены и для каждого уравнения рассчитывается оптимальная величина заказа Soj. Если величины Soj находятся внутри граничных значений j-й партии, то они сохраняются для дальнейших сравнительных расчетов. Если нет, то расчеты общих издержек производятся для граничных значений j-ой цены и они учитываются при сравнении издержек.
 | |||
 |
Рис. 6.3. Зависимости, отражающие скидки с цены продукции:
а - дискретная ("ступенчатая") зависимость и ее аппроксимация прямой, формула (6.14);
б - нелинейные зависимости скидок, формула (6.15): 1 (а0 = 0,7; в0 = 0,99);
2 (а0 = 0,5; в0 = 0,99).
Таблица 6.2
Изменение цены и затраты на хранение от размера партии
| Номер | Размер партии поставки, ед. | Цена единицы товара Cnj, у. е. | Доля от цены на хранение единицы товара i | Затраты на хранение единицы товара Cxj, у. е. |
| 1 - 9999 | 2,5 | 0,24 | 0,6 | |
| 10000-19999 | 2,0 | 0,20 | 0,4 | |
| 20000 и более | 1,5 | 0,20 | 0,3 |
Запишем систему уравнений для общих издержек с учетом данных, приведенных в табл.6.2, а также следующих условий [17]: А=106 ед.; С0=2,5 у.е.; β = 0,5
|


 (6.13)
(6.13)

С помощью формулы (6.3) находим оптимальные величины заказа для каждой партии: S01=9130 ед.; S02=11180 ед.; S03=12910 ед.
Поскольку величины заказов S 01 и S 02 лежат в пределах граничных значений, то они должны быть выбраны в качестве оптимальных. Для третьей величины S 03 ограничение на размер партии не соблюдается, поэтому рассчитываются минимальные общие издержки на границе при S = 20 000 ед.

Проведя аналогичные расчеты для второго уравнения при S02, т.е. для оптимальной партии, находим С2min = 2000450 у.е.
Следовательно, наименьшие общие затраты, связанные с запасами, соответствуют величине партии S= 20000 ед.
При увеличении количества ступеней «лестницы скидок», вместо системы уравнений (6.13) используются непрерывные зависимости, рис. 6.3.,
 (6.14)
(6.14)
или
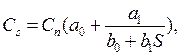 (6.15)
(6.15)
где γ, ai, bi - коэффициенты.
Рассмотрим пример определения Cn и коэффициента γ уравнения (6.14) на основании данных, приведенных в табл. 6.3.
Таблица 6.3
Скидки с цены за объем закупок [2]
| Расходы, дол. | Объем закупок, ед. |
| 5,0 | 1-99 |
| 4,5 | 100-200 |
| 4,0 | 201-300 |
| 3,5 | 301-400 |
| 3,0 | 401-500 |
Из рис.6.3. видно, что можно применить разные зависимости: по минимуму, по максимуму или средней величине объема закупок при одинаковой цене за единицу товара. Если выбрана зависимость для максимальных значений, то в качестве опорных точек могут быть взяты любые значения из правого столбца таблицы, например 99 ед. и 300 ед. Тогда, уравнения для определения Cn и γ запишутся в виде
5 = C n (1- γ · 99),
4 = C n (1- γ · 300).
После преобразований находим Cn =5, 492, γ = 0,0009 , т.е. Cs = 5,492 (1-0,0009 S), 1 £ S < 1110.
Рассмотрим зависимость (6.15), рис.6.3. б. Коэффициент a0 отражает предельное снижение цены единицы продукции Cп при S ®¥. Допустим, что коэффициент а1 = 1 – а 0.
Коэффициенты b0 и b1 позволяют охарактеризовать изменения кривой Cs. Предположим, что 0 < b0 < 1 и коэффициенты b0 и b1 связаны соотношением b1 = 1 - b0 .
В табл. 6.4. приведены значения функции Cs при Cn = 1 для различных величин заказа S (от 10 до 500), при а 0 =0,7 и а 0 =0,5, а также различных коэффициентах b 0 . Из анализа данных табл. 6.4. следует, что функция (6.15) позволяет довольно гибко учитывать зависимость между величиной скидки и объемом заказа.
Для примера рассчитаем коэффициенты аi и bi по данным табл. 6.3.
Поскольку предельное уменьшение цены Cmin = 3 дол., то а0 = 3/5=0,6 и, соответственно, а1 =0,4.
Для определения коэффициента b0 воспользуемся значениями S = 250 ед., Cs = 4,0 долл., и после подстановки в уравнение (6.15) получим:

откуда b0 =0,996, b1 = 1 - b0 = 0, 004.
Определим оптимальный размер заказа с учетом скидки по формуле (6.14) и введения коэффициента β при учете оплаты за хранение. Тогда, критериальное уравнение запишется в виде
 , (6.16)
, (6.16)
Приравняв частную производную  , после преобразований находим
, после преобразований находим
aS3 + bS2 + d = 0, (6.17)
где: а = 2βγСni; b = -βСni; d = C0A.
Таблица 6.4
Изменение величины скидки в зависимости от объема заказа,
формула (6.15)
| Заказ S, шт. | Коэффициенты b0 (при a0=0,7) | Коэффициенты b0 (при a0=0,5) | ||||
| 0,7 | 0,9 | 0,99 | 0,7 | 0,9 | 0,99 | |
| 0,780 | 0,860 | 0,975 | 0,635 | 0,751 | 0,959 | |
| 0,719 | 0,751 | 0,901 | 0,532 | 0,584 | 0,836 | |
| 0,710 | 0,728 | 0,850 | 0,516 | 0,546 | 0,751 | |
| 0,705 | 0,714 | 0,800 | 0,508 | 0,524 | 0,667 | |
| 0,703 | 0,710 | 0,775 | 0,505 | 0,516 | 0,625 | |
| 0,702 | 0,707 | 0,760 | 0,504 | 0,512 | 0,600 | |
| 0,702 | 0,705 | 0,750 | 0,503 | 0,509 | 0,583 |
Для решения кубического уравнения (6.17) можно воспользоваться аналитическим или численным (итерационным) способами.
Аналитический способ. Один из вариантов сводится к следующему:
1. Вводится новая переменная y = S+(b\3a).
2. При подстановке в уравнение (6.17), после преобразований находим:
y3 + 3py + 2q = 0, (6.18)
где p = -b2/9a2; 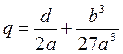
3. Число действительных корней уравнения (6.18) зависит от знака дискриминанта
D = q2 + p3
При D>0 действительный корень равен (формула Кардана)
 , (6.19)
, (6.19)
При D < 0 для определения корней уравнения (6.18) используются специальные формулы.
Приближенный способ (метод итераций). Запишем уравнение (6.17) в виде
 , (6.20)
, (6.20)
где S0 рассчитывается по формуле (6.12).
Подставив в правую часть S=S0, находим первое приближение S1 и сравним с S0, затем подставляем S=S1 и находим S2 и т.д. Процесс повторяется несколько раз до достижения заданной точности.
Пример. Определим оптимальную величину заказа при учете скидок, формула (6.14), и следующих исходных данных: А=1200 ед., С0=60,8 у.е.; Сn=29,3 у.е., i=0,22; β=0,5 и γ=0,001. Тогда, уравнение суммарных затрат запишется в виде
 , (6.21)
, (6.21)
Для исследования зависимости CΣ=f(S), выполним вспомогательные расчеты (см. табл. 6.5) и построим график CΣ=f(S), рис.6.4. Из рис.6.4 видно, что учет скидок приводит к изменению традиционной зависимости CΣ=f(S); в данном случае у зависимости суммарных затрат CΣ наблюдается не только минимум, но и максимум. Это говорит о том, что если величина заказа ограничена, например S<SA (см. рис.6.4), то оптимальное значение S0 совпадает с минимумом функции CΣ=f(S).
Для определения S0 воспользуемся формулой (6.12)

Тогда первое приближение

Второе приближение

Продолжив вычисления, находим S3=191,5; S4= 192,2. В виду того, что ΔS=|S4-S3|<1, примем Sопт.=192.
Пример 2. Определены зависимости составляющих суммарных затрат СS при следующих исходных данных: С0 = 19 долл.; А = 2400 шт.; b = 0,5; i = 0,2 [2]. Скидки учтены в виде зависимости (6.14); Сn = 5,492 дол.; γ = 0,0009. Таким образом, выражение для суммарных затрат запишется в виде:

 (6.22)
(6.22)
Таблица 6.5
Расчет составляющих и суммарных затрат на выполнение заказа с учетом скидок на величину заказа, формула (6.21)
| Величина заказа, S ед. | Затраты на выполнение заказа | Затраты на хранение С х | Суммарные затраты С S | ||
| Без учета скидки | С учетом скидки | Без учета скидки | С учетом скидки | ||
| 729,6 | 322,0 | 290,1 | 1051,6 | 1019,7 | |
| 486,4 | 483,5 | 411,0 | 969,9 | 897,4 | |
| 364,8 | 644,6 | 515,7 | 1009,4 | 880,5 | |
| 291,8 | 805,5 | 604,3 | 1097,3 | 896,1 | |
| 243,2 | 967,0 | 676,8 | 1210,2 | 919,8 | |
| 182,4 | 1289,2 | 773,3 | 1474,6 | 955,7 | |
| 145,9 | 1611,5 | 805,3 | 1757,4 | 951,1 | |
| 121,6 | 1933,8 | 773,3 | 2055,4 | 895,1 | |
| 104,2 | 2256,1 | 676,8 | 2360,3 | 781,0 | |
| 91,2 | 2578,4 | 515,7 | 2669,6 | 606,9 |
На рис.6.5 представлены составляющие затрат, связанные с заказом и хранением, а также с учетом и без учета скидок на цену товара от величины заказа (вспомогательные расчеты – табл. 6.6).
В отличие от ранее приведенных зависимостей на рис.6.1 и рис.6.4 у СS = f(S) при учете скидок не наблюдается минимума. Это имеет принципиальное значение, поскольку в данном случае невозможно рассчитать значение EOQ – оптимальную величину заказа и она должна быть определена как «экономичная» величина исходя из других критериев или ограничений.
Таблица 6.6
Расчет составляющих суммарных затрат с учетом скидок на величину заказа, формула (21)
| Величина заказа , S ед. | Затраты на выполнение заказа | Затраты на хранение С х | Суммарные затраты С S | ||
| Без учета скидки | С учетом скидки | Без учета скидки | С учетом скидки | ||
| 54,9 | |||||
| 109,8 | 90,1 | 337,8 | 318,1 | ||
| 164,8 | 120,3 | 318,8 | 272,3 | ||
| 219,7 | 140,6 | 333,7 | 254,6 | ||
| 91,2 | 274,6 | 151,1 | 365,8 | 242,3 | |
| 76,0 | 329,5 | 151,7 | 405,5 | 227,7 | |
| 65,1 | 384,4 | 142,4 | 449,5 | 207,5 | |
| 57,0 | 439,4 | 132,2 | 496,4 | 180,2 |
| <== предыдущая лекция | | | следующая лекция ==> |
| Елементи договору простого товариства | | | Підстави виникнення зобов'язань із публічної обіцянки винагороди |