
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Розділ II. ЗОБОВ'ЯЗАННЯ З ОДНОСТОРОННІХ ДІЙ
Дата добавления: 2015-10-15; просмотров: 644
|
|
1. Атрохов Н.А. О задаче коммивояжера // Повышение эффективности и качества автотранспортного обслуживания. – М.: МАДИ, 1989. – с. 72-74.
2. Бауэрсокс Дональд Дж., Клосс Дейвид Дж. Логистика: интгрированная цепь поставок. – М.: «Олимп – Бизнес», 2001 – 640 с.
3. Беленький А.С. Исследование операций в транспортных системах: идеи и схемы методов оптимизации планирования. – М.: Мир, 1992. – 582 с.
4. Бережной В. И., Порохня Т. А., Цвиринько И. А. Управление материальными потоками микрологической системы автотранспортного предприятия. – Ставрополь.: СевКаз ГТУ, 2002. – 198с.
5. Гаджинский А.М. Логистика: Учебник для высших и средних учебных заведений. – М.: ИВЦ «Маркетинг», 2000. – 375 с.
6. Гаджинский А. М. Практикум по логистике. – 2-е изд., перераб. и доп. – М.: Издательско-книготорговый центр «Маркетинг», 2001. – 180 с.
7. Джонсон Дж. С. и др. Современная логистика, 7-е издание. – М.: Издательский дом «Вильямс», 2002 – 624 с.
8. Кожин А.П., Мезенцев В.Н. Математические методы в планировании и управлении грузовыми автомобильными перевозками: Учеб. для вузов. – М.: Транспорт, 1994. – 304 с.
9. Косова Л. Н., Мужейникова Т. В. Логистика: Учебн. пособие. – М.: Изд-во МГУП, 1999.- 79 с.
10. Линдерс Майкл Р., Фирон Харольд Е. Управление снабжением и запасами. Логистика – СПб.: ООО «Виктория плюс», 2002 – 768с.
11. Логистика: Учебное пособие / Под ред. Б.А. Аникина. – М.; 2000. – 352 с.
12. Лукинский В. С., Зайцев Е. И. Прогнозирование надежности автомобилей – Л.: Политехника, 1991 – 220с.
13. Лукинский В.С. и др. Логистика автомобильного транспорта. Концепция, методы, модели – М.: Финансы и статистика, 2000.
14. Лукинский В. С. и др. Оценка влияния размещения складской сети на транспортные расходы. Экономика и менеджмент на транспорте: Сб. научн. тр.: Вып.2. - СПб.: СПбГИЭУ, 2002. - с.99 - 106
15. Международные автомобильные перевозки: Учеб. пособие / Под ред. Ю.С. Сухина, В.С. Лукинского. – СПб.: СПбГИЭУ, 2001. – 204 с.
16. Малевич Ю. В. Вероятностный подход к определению уровня материально-производственных запасов. Экономика и менеджмент на транспорте: Сб. научн. тр.: Вып.2. - СПб.: СПбГИЭУ, 2002. - с.115-117
17. Неруш Ю.М. Логистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2000. – 389 с.
18. Николайчук В. Е. Логистика: СПб.: Питер, 2001 – 160 с.
19. Основы логистики: Учебное пособие / Под ред. Л.Б. Миротина и В.И. Сергеева – М.: ИНФРА-М, 2000. – 200 с.
20. Практикум по логистике: учебное пособие / Под ред. Б.А. Аникина – М.: ИНФРА-М, 1999. – 270 с.
21. Родников А. Н. Логистика: Терминологический словарь. – М.: Экономика, 1995 – 251 с.
22. Рыжиков Ю. И. Теория очередей и управление запасами – СПб.: Питер, 2001 – 384 с.
23. Сергеев В.И. Менеджмент в бизнес-логистике. – М.:Филинъ, 1997. – 772 с.
24. Смехов А.А. Основы транспортной логистики. – М.: «Транспорт», 1995 – 197 с.
25. Транспортная логистика. Учебное пособие / Под ред. Л.Б. Миротина – М.: МГАДИ (ТУ), 1996. – 211 с.
26. Уваров С.А. Логистика: общая концеция, теория и практика. - СПб.: "ИВЕСТ-НП", 1996. - 232 с.
27. Шульга Г. В., Лукинский В. В. Выбор варианта доставки контейнеров. Экономика и менеджмент на транспорте: Сб. научн. тр.: Вып.2 - СПб: СПбГИЭУ, 2002 - с.160-163.
28. Щетина В. А., Лукинский В. С., Сергеев В. И. Снабжение запасными частями на автомобильном транспорте – М.: Транспорт, 1988 – 109с.
29. Экономика и организация внешнеторговых перевозок: Учебник / Под ред. проф. К. В. Холопова. - М.: Юристъ, 2000. - 684 с.
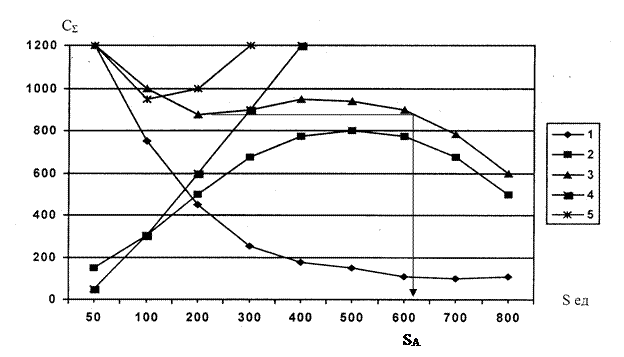
Рис. 6.4. Суммарные затраты на выполнение заказа с учетом скидок на величину заказа, зависимость (6.21.):
1 - затраты на выполнение заказа; 2 - затраты на хранение с учетом скидок; 3 - суммарные затраты с учетом скидок; 4 - затраты на хранение (без учета скидок); 5 - суммарные затраты без учета скидок.
Рассмотрим вариант при использовании зависимости (6.15). Тогда уравнение (6.15) запишется в виде:
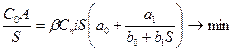 , (6.23)
, (6.23)
Примем, что а0=0,6; а1=0,4; b0=0,996; b1=0,004.
Исследуем зависимость CΣ=f(S). При подстановке исходных данных: С0=19 долл., А0=2400; β=0,5; Сn=5 долл.; i=0,2 находим
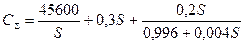 , (6.24)
, (6.24)
Вспомогательные расчеты приведены в табл.6.7. Графики составляющих и суммарных затрат на рис. 6.6. Из рис.6.6 видно, что при учете скидок минимум СΣ смещается в область больших величин заказа S, при этом сохраняется подобие с зависимостью СΣ, рассчитанной без учета скидок.
Для точного определения оптимальной величины заказа воспользуемся стандартной процедурой, т.е. найдем Sопт. из решения уравнения dCΣ/dS=0, где СΣ описывается выражением (6.1). После преобразований находим
KS4 + LS2 + M2 + NS + Q = 0 (6.25)
где K = βcniaob12; L = 2βcniaobob1; M = βcniaobo2 + βbocnia1 – coAb12; N = -2coAbob1; Q = -cAbo2.
Анализ показал, что наиболее приемлемым является приближенный способ, при этом итерационное уравнение можно записать в виде:
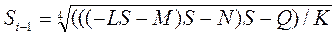 (6.26)
(6.26)
Рассчитаем коэффициенты уравнения (6.25):
К=0,5·5·0,2·0,6·0,0042=4,8·10-6
L=2·0,5·5·0,2·0,6·0,996·0,004=2,39·10-3
M=0,5·5·0,2·0,6·0,9962+0,5·0,996·5·0,2·0,4 - 19·2400·0,0042= -0,2328
N= -2·19·2400·0,996·0,004= -363,3
Q= -19·2400·0,9962= - 45236
При подстановке численных значений в уравнение (6.26) получим
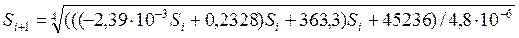 (6.27)
(6.27)
В качестве начальной итерации примем S0=300. При подстановке в (6.27) находим S1= 389,6.
Последующие значения: S2=360,1; S3=374,7; S4=368,2; S5=371,3; S6=370. Следовательно, шестая итерация позволяет получить приемлемую точность Δ=|S6 – S5|~1.
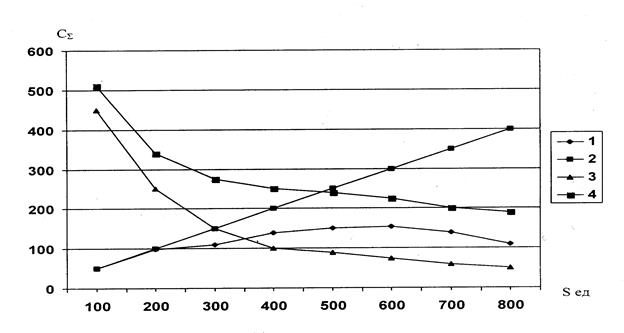
Рис. 6.5. Составляющие суммарные затраты на выполнение заказа с учетом скидок на величину заказа, зависимость (6.22):
 1 - затраты на хранение с учетом скидок; 2 - затраты на хранение (без учета скидок); 3 - затраты на выполнение заказа; 4 - суммарные затраты.
1 - затраты на хранение с учетом скидок; 2 - затраты на хранение (без учета скидок); 3 - затраты на выполнение заказа; 4 - суммарные затраты.
Рис. 6.6. Составляющие суммарные затраты на выполнение заказа с учетом скидок на величину заказа, зависимость (6.24):
1 - затраты на выполнение заказа; 2 - затраты на хранение; 3 - суммарные затраты; 4 - суммарные затраты с учетом скидки.
Таблица 6.7
Расчет составляющих и суммарных затрат с учетом скидок на величину заказа
| Величина заказа , S ед. | Затраты на выполнение заказа | Затраты на хранение С х | Суммарные затраты С S | ||
| Без учета скидки | С учетом скидки | Без учета скидки | С учетом скидки | ||
| 44,3 | 500,3 | ||||
| 63,8 | 367,8 | ||||
| 82,3 | 310,3 | ||||
| 182,4 | 307,4 | 282,4 | |||
| 152,0 | 117,3 | 269,3 | |||
| 114,0 | 150,8 | 264,8 | |||
| 91,2 | 183,4 | 341,2 | 274,6 | ||
| 215,3 | 291,3 | ||||
| 65,1 | 246,9 | 415,1 | 312,0 |
В заключении сопоставим различные варианты расчета EOQ – экономического размера заказа. Для проведения расчетов были выбраны следующие исходные данные:
· А = 2400 ед., С0 = 19 долл., Сn = 5 долл., i = 0,2;
· коэффициент β, учитывающий затраты на хранение, принимался равным 0,25, 0,5 и 0,75;
· значения цены Сn с учетом скидок были взяты из табл.6.3. и составили 5, 4 и 3 долл.; при расчете суммарных затрат с учетом скидок (дискретная зависимость) учитывались затраты на заказ и хранение;
· учет снижения цены Сn производился для двух зависимостей – линейной (уравнение (6.14), γ=0,0009) и нелинейной (уравнение (6.15),
a0=0,6, b0=0,996).
Таблица 6.8
Результаты расчета оптимальной величины заказа
| Варианты | Коэффициент β | ||
| 0,25 | 0,5 | 0,75 | |
| Основная модель (формула Уилсона) | 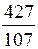
| 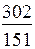
| 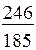
|
| С учетом скидок (дискретная зависимость) · СS1(<200) | 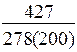
| 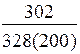
| 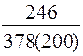
|
| · СS2(201-400) | 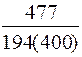
| 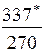
| 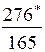
|
| · СS3(401-600) | 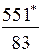
| 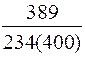
| 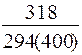
|
| С учетом скидок · линейная зависимость · нелинейная зависимость | 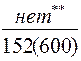
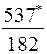
| 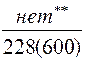
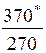
| 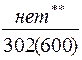
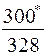
|
| Примечания: *) в числителе – величина заказа, в знаменателе – суммарные затраты; **) отсутствует оптимальное значение |
Анализ результатов табл. 6.8 позволяет констатировать:
· величина заказа S0 для различных вариантов расчета колеблется в широких пределах: от минимального значения S0min=246 ед. до максимального S0max=551 ед., т.е. более, чем в два раза;
· при β=const (например, β=0,5) колебания S0 невелики – от 302 ед. до 370 ед.;
· суммарные затраты для представленных вариантов изменяются от 83 долл. до 378 долл., т.е. более чем в четыре раза.
· при β=const (β=0,5) диапазон значений уже – от 151 до 328 долл.
Таким образом, учет особенностей формулы Уилсона и ее модификаций позволяет повысить точность расчета путем выбора вариантов наиболее полно соответствующей системе осуществления заказов и хранения партий продукции конкретного предприятия.
Приведенные варианты определения оптимальной величины заказа расширяют границы ограничений принятых при выводе классической формулы Уилсона-Харриса и позволяет учесть влияние разных факторов, связанных с затратами на хранение партии товара на складе и скидок с оптовой цены в зависимости от размера заказываемой партии. С теоретической точки зрения при различном сочетании составляющих уравнения (6.1) возможно получение различных аналитических зависимостей – уравнений третьего, четвертого и более высоких порядков, в частности, кубического уравнения аналогичного уравнению Ван-дер-Вальса, используемого в термодинамике.
Министерство образования Республики Беларусь
| <== предыдущая лекция | | | следующая лекция ==> |
| Розділ II. ЗОБОВ'ЯЗАННЯ З ОДНОСТОРОННІХ ДІЙ | | | Поняття і значення зобов'язань з відшкодування шкоди |