Ранг матрицы
Рангом называется наибольший порядок неравного нулю минора, т.е., порядок наибольшего определителя, неравного нулю, «вырезанного» из матрицы. Пример 5 Найти ранг Решение Определитель матрицы Следовательно
Пример 6 Найти ранг
1.5. Обратная матрица
Обратная матрица существует только у квадратной матрицы и только тогда, когда её определитель не равен нулю. Она находится по формуле:
Например: Знаки определяются по суммам индексов: если чётное – плюс, а если нечётное, то минус.
Пример 7 Найти обратную матрицу
Пример 8 Найти обратную матрицу Решение
Механически: у матрицы второго порядка на главной диагонали элементы местами меняются, а на побочной знаки меняются.
|
, т.к. первая и третья строки пропорциональны, поэтому 
. 
.
, т.к. минор второго порядка не равен нулю.
. 
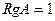. Наибольший минор первого порядка.
, если 
.
; 
.
.
.
, 
. 
.
