Первый замечательный предел
Следствия: Эквивалентность бесконечно малых величин (при
Нижеследующие пределы можно решать с помощью 1-го замечательного предела, с помощью эквивалентности бесконечно малых величин, а также по правилу Лопиталя. Пример 68
Пример 69
Второй замечательный предел
Пример 70
Пример 71 Пример 72
Пример 73 Пример 74
Следствия из второго замечательного предела
Односторонние пределы
Пример 75 Найти предел слева функции Решение Пример 76 Найти предел справа функции Решение Пример 77 Найти предел слева функции
|
.
, 
, 
.
):
, 
, 
,
, 
, 
.
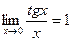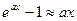или 
или 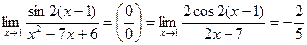(применим сначала эквивалентность, затем правило Лопиталя):
или 
.
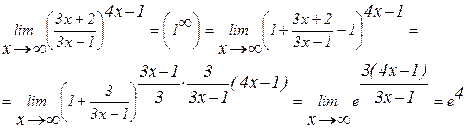
. В нижеследующих примерах нет неопределенности 
.
.
.
.
, 
, 
, 
, 
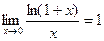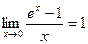- предел слева, 
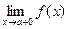- предел справа.
при 
.
.
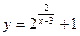при 
.
.
при 
.
