Кривые второго порядка
Пример 37 Что определяет уравнение:
1) 2) 3)
4) 5) параболы:
Фокусы параболы находятся на осях симметрии.
6) 7)
Пример 38 Найти фокусы эллипса Решение
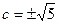Пример 39 Найти эксцентриситет гиперболы Решение
Пример 40 Найти центр и радиус окружности Решение Сгруппировав переменные и выделив полный квадрат, получим:
Аналитическая геометрия в пространстве
|
− окружность, где 
− центр, 
− радиус.
- окружность, где 
− центр, 
− эллипс, 
− полуоси
, если 
− большая полуось 
, если 
− большая полуось
− половина расстояния между фокусами
(либо 
) – эксцентриситет
− гипербола, 
, 
− асимптоты гиперболы, 
симметрична относительно 
,
симметрична относительно оси 
.
− нижняя часть параболы
− верхняя половина окружности
.
, 
, 
.
, 
.
.
, 
, 
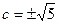- центр, 
- радиус.
