Решение. Пример 78 Найти точки разрыва функции
Пример 78 Найти точки разрыва функции Решение Пример 79 Найти точки разрыва функции Решение Дифференциальное исчисление функции одной переменной
Производная функции
Производной функции называется Таблица производных:
Основные правила дифференцирования:
1) 2)
Логарифмическое дифференцирование
а) применяется при произведении и частном более двух функций, б) при дифференцировании сложной показательной функции,
Производную сложной показательной функции можно найти по формуле:
6.3 Дифференцирование функции, заданной в параметрическом виде.
Пример 80 Найти производную функции Решение
Дифференцирование сложной функции
Пример 81 Пример 82 Пример 83 Пример 84 Пример 85
Дифференцирование неявной функции
Пример 86
|
.
.
, 
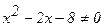, точки разрыва 
.
.
- точка разрыва 2-го рода, так как 
.
.
3) 
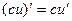
4) 
, 
, 
.
, 
.
.
, 
.
.
.
, 
.
.
.
.
.
.
, 
,
, 
.
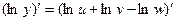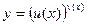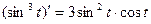