Прямая в пространстве
1) Каноническое уравнение прямой:
где 2) Параметрическое уравнение:
3) Общее уравнение прямой:
4) Уравнение прямой проходящей через две заданные точки:
5) Угол между двумя прямыми в пространстве:
6) Условие параллельности двух прямых в пространстве
7) Условие перпендикулярности двух прямых в пространстве:
8) Угол между прямой и плоскостью
9) Условие параллельности прямой и плоскости:
10) Условие перпендикулярности прямой и плоскости:
11) Условие пересечения прямых в пространстве:
Чтобы прямые в пространстве пересекались, они должны лежать в одной плоскости, поэтому
12) Расстояние от точки Пример 54 Написать уравнение плоскости, перпендикулярной прямой Решение Пример 55 Найти точку пересечения прямой Решение Перепишем уравнение прямой в параметрическом виде и подставим вместо переменных в уравнение плоскости их выражения через параметр:
Подставив в параметрическом уравнении прямой вместо параметра найденное значение, получим координаты искомой точки, Пример 56 Составить каноническое уравнение прямой, проходящей через точку М0(2; 0; -3) и параллельно прямой Решение Направляющий вектор данной прямой будет также направляющим и для искомой прямой, т.е. Пример 57 Вычислить угол между прямой Решение Найдем угол между направляющим вектором прямой и нормальным вектором плоскости.
Пример 58 При каких значениях Решение По признаку перпендикулярности прямой и плоскости:
Пример 59 Пересекаются ли прямые Решение
|

 ,
, - направляющий вектор прямой,
- направляющий вектор прямой,  - координаты точки, принадлежащей прямой.
- координаты точки, принадлежащей прямой.

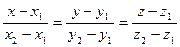



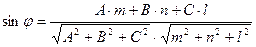


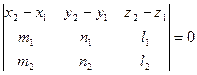
 до прямой, проходящей через точку
до прямой, проходящей через точку  с направляющим вектором
с направляющим вектором  .
.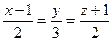 и проходящей через точку с координатами (2; 0; 1). Направляющий вектор данной прямой может служить нормальным вектором для искомой плоскости, т.е.
и проходящей через точку с координатами (2; 0; 1). Направляющий вектор данной прямой может служить нормальным вектором для искомой плоскости, т.е.  , тогда
, тогда 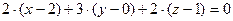 ,
,  .
. и плоскости
и плоскости 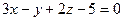 .
. ,
,  , отсюда
, отсюда  .
.
 .
. . Напишем каноническое уравнение для искомой прямой:
. Напишем каноническое уравнение для искомой прямой:  .
. и плоскостью
и плоскостью  .
.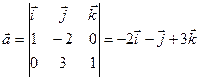 ,
,  ,
,  .
. и
и  прямая
прямая  перпендикулярна к плоскости
перпендикулярна к плоскости  ?
? , отсюда
, отсюда .
.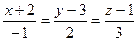 и
и  ?
? . Не пересекаются.
. Не пересекаются.


