Работа внешних и внутренних сил при растяжении (сжатии). Потенциальная энергия деформации
При растяжении (сжатии) внешние силы совершают работу вследствие перемещения точек их приложения (рис. 2.10 а). Вычислим работу статически приложенной внешней силы, т. е. такой силы, которая растет в процессе деформации от нуля до своего конечного значения с весьма небольшой скоростью.
Рис. 2.10. Элементарная работа dW внешней силы F на перемещении
Но между
Подставляя это значение в формулу (2.22), получаем
Полную работу силы получим, интегрируя это выражение в пределах от нуля до окончательного значения перемещения
Таким образом,
т. е. работа внешней статически приложенной силы равна половине произведения окончательного значения силы на окончательную величину соответствующего перемещения.
Рис. 2.11.
Графически работа силы F выражается (с учетом масштабов) площадью ОСВ диаграммы, построенной в координатах Отметим, что работа силы
При деформации совершают работу не только внешние силы, но и внутренние (силы упругости). Элементарная работа внутренних сил (для элемента dz) вычисляется по формуле (рис. 2.11):
где N – внутреннее усилие (продольная сила); ∆ (dz) – удлинение элемента. Но, согласно закону Гука имеем
Полную работу внутренних сил получим, интегрируя обе части формулы (26) по длине всего стержня
Если N, E и A постоянны, то
где Величина, равная работе внутренних сил, но имеющая противоположный знак, называется потенциальной энергией деформации. Она представляет собой энергию, накапливаемую телом при деформации. Таким образом, для стержня постоянного сечения при продольной силе, имеющей одно и то же значение во всех поперечных сечениях, потенциальная энергия при растяжении (сжатии) определяется по формуле
Потенциальная энергия, отнесенная к единице объема материала, называется удельной потенциальной энергией:
или
При объемном напряженном состоянии удельная потенциальная энергия получится как сумма трех слагаемых:
Используя обобщенный закон Гука, получаем
Из этой формулы как частный случай, полагая одно из главных напряжений равным нулю, легко получить формулу для плоского напряженного состояния.
|


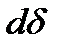 равна
равна . (2.22)
. (2.22) и F существует зависимость (закон Гука)
и F существует зависимость (закон Гука)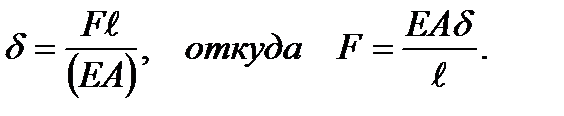
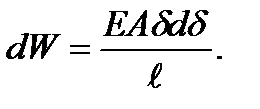
 :
: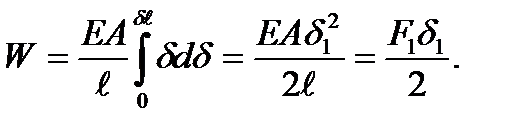
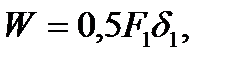 (2.23)
(2.23)
 (рис. 2.11, б).
(рис. 2.11, б). неизменной по значению, на перемещении
неизменной по значению, на перемещении  равна
равна (2.24)
(2.24)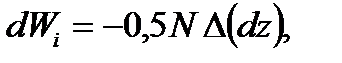 (2.25)
(2.25) Следовательно,
Следовательно,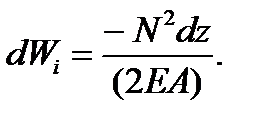 (2.26)
(2.26)
 . (2.27)
. (2.27) , (2.28)
, (2.28) – удлинение стержня.
– удлинение стержня. . (2.29)
. (2.29) (2.30)
(2.30) так как
так как  или
или  (2.31)
(2.31) (2.32)
(2.32) (2.33)
(2.33)


