Ведомое колесо
Допущения: 1. Колесо катится равномерно с поступательной скоростью U и угловой скоростью ω к. 2. Грунт твердый, недеформируемый. 3. Шина испытывает только радиальную (нормальную) и продольную (касательную) деформации в плоскости качения. 4. Трением в подшипниках качения колеса пренебрегаем. 5. Деформации считаем независимыми друг от друга. На колесо действуют следующие силы: 1. Со стороны автомобиля: Gк – нормальная нагрузка на колесо; Рк – толкающая сила со стороны рамы. 2. Со стороны дороги: Zк – нормальная реакция, которую называем равнодействующей нормальных реакций. Она приложена в центре давления К; Хк – равнодействующая касательных реакций, она приложена в плоскости дороги. Как видно из рис. 4, силы Gк и Zк смещены относительно центра колеса: а) Gк – на величину «С» за счет касательной (продольной или тангенциальной) деформации шины (λ); б) Zк - на величину «α» вследствие внутреннего трения в шине – радиальной деформации и гистерезиса. Пользуясь рис. 4, составим уравнения равновесия
Составим и решим уравнение моментов
где rд – динамический радиус колеса;
Отсюда получим
Реакция Хк (рис. 4) есть не что иное, как сила трения. Ее предельное значение определяется по формуле
где φ – коэффициент сцепления. Это очень важная формула, так как она определяет предельное значение: а) реализуемый силы тяги (без юза и буксования); б) реализуемой тормозной силы (без абсолютного скольжения колеса по дороге при его торможении, что является эффективным режимом его торможения).
Рис. 4. Качение ведомого колеса
Рис. 5. Гистерезис в шине
Потери в упругом автомобильном колесе
Академиком Чудаковым Е.В. установлена следующая ранее приведенная нами зависимость для определения радиуса качения колеса
Все деформации в упругой шине сопровождаются потерями, которые можно описать формулой
где Ny – потери на касательную деформацию шины; Nr – потери на радиальную деформацию шины.
Вернемся к ведомому колесу, для которого: 1. Рк > 0 и Мк = 0. 2. Мгновенный центр лежит ниже плоскости дороги. 3. Радиус качения колеса определяется по формуле (5).
Определим скорость упругого скольжения Vуп. Переносная скорость равна U = ω к rk .. Относительная скорость равна Uо = ω к rо. Абсолютная скорость будет V = ω к rk - ω к rо = (rk - rо) ω к.
Итак Как известно, абсолютное скольжение аналогично упругому скольжению в шине, а значит оно описывается одними и теми же формулами. Следовательно, можно записать
Подставив в уравнение (9) выражение для rк (формула 5), получим
Подставив полученное выражение (10) в формулу (7), получим
Это и есть мощность упругих потерь в шине – Ny. Определим теперь гистерезисные потери – Nг. Согласно рис. 4 «а» - плечо сопротивления качению. Его произведение на Gк дает момент сопротивления качению колеса
Произведение момента сопротивления качению Mf на угловую скорость ω к и дает мощность гистерезисных потерь. В таком случае получим
В результате мы получили формулу для определения потерь в упругом автомобильном колесе
Отсюда окончательно получим
|


 ,
,
 (3)
(3) (4)
(4)

 (5)
(5) (6)
(6) (7)
(7) (8)
(8)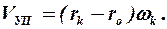 . (9)
. (9) (10)
(10)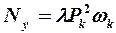 . (11)
. (11) (12)
(12) (13)
(13) (14)
(14) (15)
(15)


