Тема 6 . Показатели вариации
Вопросы к изучению 1. Понятие о вариации 2. Абсолютные и средние показатели вариации 3. Относительные показатели вариации. Тесты 1. Вариация – это: а) изменение массовых явлений во времени; б) изменение структуры статистической совокупности в пространстве; в) изменение значений признака во времени и пространстве. 2. К абсолютным показателям относятся: а) дисперсия; б) размах вариации; в) средняя арифметическая; г) коэффициент роста. 3. Базой сравнения при расчете относительных показателей вариации служит следующий показатель: а) среднее квадратическое отклонение; б) средняя арифметическая; в) размах; 4. Какой показатель вариации характеризует абсолютный размер колеблемости признака относительно средней величины: а) размер вариации; б) коэффициент вариации; в) среднее квадратическое отклонение. 5. Размах вариации представляет собой абсолютную разность между: а) максимальным значением признака и средней; б) индивидуальным значением признака и средней; в) максимальным и минимальным значением признака. 6. Среднелинейное отклонение представляет собой: а) отклонение индивидуальных значений признака от их средней; б) среднюю арифметическую из абсолютных отклонений индивидуальных значений признака от средней; в) среднюю арифметическую из отклонений индивидуального значения признака от средней. 7. Дисперсия представляет собой: а) средней размер отклонений индивидуальных значений признака от средней; б) средний квадрат отклонений индивидуальных значений признака от средней арифметической; в) средний квадрат отклонений индивидуальных значений признака от средней квадратической. 8. Правилом сложения дисперсий называют следующее соотношение: а) б) в) г) 9. Вам известны следующие виды дисперсий: а) межгрупповая; б) общая; в) взвешенная; г) простая. 10. Среднее квадратическое отклонение: а) это показатель степени однородности изучаемой совокупности; б) средняя арифметическая квадратов отклонений значений признака от средней величины; в) разность между максимальным и минимальным значениями признака; г) вариация отклонений значений признака от средней величины. 11. Коэффициент вариации характеризует: а) диапазон вариации признака; б) степень вариации признака; в) тесноту связи между признаками; г) пределы колеблемости признака. 12. Чему равна межгрупповая дисперсия, если отсутствуют различия между вариантами внутри групп? а) единице; б) нулю; в) колеблется от нуля до единицы; г) общей дисперсии; д) средней из групповых дисперсий. 13. Коэффициент детерминации измеряет: а) степень тесноты связи между исследованиями признаками; б) долю вариации признака-результата, сложившегося под влиянием изучаемого факторного признака; в) вариацию, связанную с влиянием всех остальных факторов, кроме исследуемого. 14. Если все значения признака увеличить в 16 раз, то дисперсия: а) не изменится; б) увеличится в 16 раз; в) увеличится в 256 раз; г) увеличится в 4раза. 15. Если отсутствуют различия между вариантами внутри групп, то межгрупповая дисперсия равна: а) единице; б) нулю; в) колеблется от нуля до единицы; г) общей дисперсии. Тренировочные задания: Тренировочное задание 1 По приведенным ниже данным о квалификации рабочих цеха требуется: 1) построить дискретный ряд распределения; 2) дать графическое изображение ряда; 3) вычислить показатели центра распределения, показатели вариации и формы распределения. Тарифные разряды 24 рабочих цеха: 4; 3; 6; 4; 4; 2; 3; 5; 4; 4; 5; 2; 3; 4; 4; 5; 2; 3; 6; 5; 4; 2; 4; 3. Решение тренировочного задания 1 1. Дискретный ряд распределения после группировки имеет вид
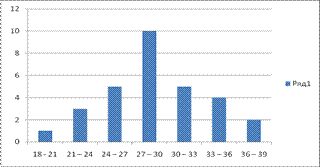
На рис. 6.1 представлено графическое изображение построенного дискретного вариационного ряда в виде полигона частот.
Рис. 6.1 Полигон распределения рабочих цеха по квалификации
Полигон частот замыкается, для этого крайние вершины соединяются с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе (то есть 3. К показателям центра распределения относятся: средняя арифметическая, мода и медиана. Среднюю арифметическую определяем по формуле:
Для расчета показателей ряда распределения удобно использовать вспомогательную таблицу.
Среднее линейное отклонение (ρ) равно:
Среднее квадратическое отклонение (σ) определяется по формуле:
Коэффициент вариации (ν) рассчитаем по формуле:
Выводы: индивидуальные значения отличаются в среднем от средней арифметической на 1, 15 разряда, или на 30, 3 %. Среднее квадратическое отклонение превышает среднее линейное отклонение в соответствии со свойствами мажорантности средних. Значение коэффициента вариации (30, 3 %) свидетельствует о том, что совокупность достаточно однородна. Тренировочное задание 2 Имеются следующие данные о возрастном составе рабочих цеха (лет): 18; 38; 28; 29; 26; 38; 34; 22; 28; 30; 22; 23; 35; 33; 27; 24; 30; 32; 28; 25; 29; 26; 31; 24; 29; 27; 32; 35; 29; 29. Для анализа распределения рабочих цеха по возрасту требуется: 1) построить интервальный ряд распределения, выделив 7 групп; 2) дать графическое изображение ряда; 3) исчислить показатели центра распределения, показатели вариации и формы распределения. Сформулировать вывод. Решение тренировочного задания № 2 1. Величина интервала группировки определяется по формуле
где n принимаем равным 7. Интервальный ряд распределения выглядит следующим образом:
2. Графически интервальный вариационный ряд может быть представлен в виде гистограммы, полигона, кумуляты. Гистограмма строится в прямоугольной системе координат. По оси абсцисс окладывают интервалы значений вариационного признака Для преобразования гистограммы в полигон частот середины верхних сторон прямоугольников соединяют отрезками прямой, и две крайние точки прямоугольников замыкаются по оси абсцисс на середине интервалов, в которых частоты равны нулю. На рис. 6.2 и 6.3 представлено графическое изображение построенного интервального вариационного ряда в виде гистограммы и полигона частот. Как видно из графика, треугольники, относящиеся к площади гистограммы и к площади полигона, попарно равны между собой, и, следовательно, площадь полигона данного вариационного ряда также совпадают.
Рис. 6.2. Гистограмма распределения рабочих цеха по возрасту
Рис. 6.3. Полигон распределения рабочих цеха по возрасту На основании построенной гистограммы графически можно определить значение моды. Для этого правую вершину модального прямоугольника соединяют прямой с правым верхним углом предыдущего прямоугольника соединяют с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения. Мода года на рис. 6.4.
Рис. 6.4. Определение моды по гистограмме На рис. 6.5 представлена кумулятивная кривая (кумулята).
Рис 6.5. Определение медианы по кумулятивной кривой Кумулята может быть использована для графического определения медианы. Для этого последнюю ординату кумуляты делят пополам 30/2=15. Через полученную точку проводят прямую, параллелую оси x, до пересечения ее с кумулятой. Из точки пересечения опускается перпендикуляр до оси абсцисс. Абсцисса точки пересечения является медианой. Линии, определяющие медиану, на рис. 6.5. Ме = 28, 8 года. 1. Расчет показателей центра распределения:
где x - среднее значение признака в интервале (центр интервала), т. е. например (18+21) / 2 = 19, 5. Для интервального вариационного ряда порядок расчета структурных средних следующий: сначала находят интервал, содержащий моду или медиану, а затем рассчитывают соответствующие значения названных показателей. Модальным в данном распределении является интервал 27-30 лет, так как наибольшее число рабочих (
Mo = 27 + 3 Медианным является тот же интервал 27-30 лет, т.к. полусумма частот 0, 5
Следовательно, вариация возраста у рабочих данного цеха не является значительной, что подтверждает достаточную однородность совокупности. Тренировочное задание 3 По данным о чистой прибыли предприятий двух районов определите: 1) дисперсии: а)общую; б) межгрупповую; в) среднюю из групповых; 2) коэффициент детерминации и эмпирическое корреляционное отношение:
Решение тренировочного задания № 3 Для расчета внутригрупповых дисперсий вычислим средние (простые) по каждому району по формуле
Рассчитываем внутригрупповые дисперсии (простые) по формуле
Рассчитаем среднюю из внутригрупповых дисперсий
Рассчитаем общую среднюю арифметическую
Рассчитаем межгрупповую дисперсию
Рассчитаем общую дисперсию по правилу сложения дисперсий
Определим коэффициент детерминации
Полученное значение показывает, что чистая прибыль на 21, 74 % зависит от территориальной принадлежности предприятий и на 78, 26 % - от внутритерриториальных возможностей. Эмпирическое корреляционное отношение составит
Что свидетельствует о среднем влиянии на чистую прибыль территориальных особенностей. Для проверки рассчитаем общую дисперсию по обычной формуле
Задания для самостоятельной работы Задание № 1 По данным о распределении сотрудников коммерческого банка по стажу работы определите размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
Задание № 2 Определите дисперсию, квадратическое отклонение и коэффициент вариации по данным таблицы:
Задание № 3 Средняя урожайность зерновых культур в двух районах за 2006 – 2010 гг. характеризуется следующими данными, ц/га:
Рассчитайте коэффициент вариации. Определите, в каком районе урожайность зерновых культур более устойчива?
Задание № 4 Предприятия одной из отраслей сгруппированы по стоимости реализованной продукции и услуг за год. Результаты представлены в следующей таблице:
Определите: 1) среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию (по правилу сложения дисперсий); 2) эмпирическое корреляционное отношение. Задание № 5 Определите дисперсию и среднее квадратическое отклонение, если известно, что квадрат отклонений индивидуальных значений признака от некоторой величины А равен 1285, а разность между величиной А и средней равна 18. Задание № 6 По данным микропереписи 2010 г. получено следующее распределение населения, проживающего в месте постоянного жительства не с рождения:
Определите среднее квадратическое отклонение продолжительности проживания в месте постоянного жительства.
Задание № 7 Определите общую дисперсию по формуле
Рассчитать коэффициент вариации.
|



 ;
; 
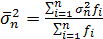 ;
; 
 .
. 


 = 2 и
= 2 и 
 = 6).
= 6).
 =
= 
 равна 4-му разряду (4-й разряд встречается 9 раз, т.е. это наибольшая частота).
равна 4-му разряду (4-й разряд встречается 9 раз, т.е. это наибольшая частота). равна 4-му разряду (так как номер 12 и 13 соответствуют 4-му разряду).
равна 4-му разряду (так как номер 12 и 13 соответствуют 4-му разряду).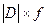



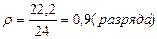






 , причем число интервалов целесообразно увеличить на два (по одному в начале и в конце имеющегося ряда) для удобства преобразования гистограммы в полигон частот. На отрезках (интервалах) строятся прямоугольники, высота которых соответствует частоте (
, причем число интервалов целесообразно увеличить на два (по одному в начале и в конце имеющегося ряда) для удобства преобразования гистограммы в полигон частот. На отрезках (интервалах) строятся прямоугольники, высота которых соответствует частоте ( .
.





 (лет),
(лет), = 10) находится в этом интервале. Значение моды определяется по формуле
= 10) находится в этом интервале. Значение моды определяется по формуле


 находится в этом интервале. Значение медианы определяем по формуле
находится в этом интервале. Значение медианы определяем по формуле

 Для расчета показателей вариации составляется вспомогательная таблица.
Для расчета показателей вариации составляется вспомогательная таблица.
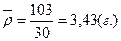


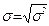 =
= 


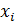
 =
= 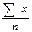
 =
= 
 =
= 
 = 8 млн.р.
= 8 млн.р.
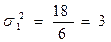



 =
= 
 = 7, 25 (млн.р.)
= 7, 25 (млн.р.)





 по данным таблицы:
по данным таблицы:


