Тема 7. исследование динамики и структуры явления
Вопросы к изучению 1. Базисная и цепная форма расчета показателей динамики 2. Интервальный и моментный ряды динамики. Расчет среднего уровня ряда в них. 3. Преобразование рядов динамики. Выявление
Тесты 1. Ряд динамики характеризует: а) структуру по какому-либо признаку; б) изменение характеристики совокупности в пространстве; в) изменение характеристики совокупности во времени; г) изменение характеристики совокупности в пространстве и времени. 2. Уровень ряда динамики: а) это определенное значение варьирующего признака в совокупности; б) величина показателя на определенный период времени; в) величина связи показателя и времени. 3. Средний уровень интервального ряда определяется как средняя: а) арифметическая; б) гармоническая; в) хронологическая; 4. Если сравнивают смежные уровни ряда динамики, показатели называют: а) цепными; б) базисными; в) аналитическими; г) функциональными. 5. Абсолютный прирост рассчитывают: а) как отношение уровней ряда; б) разность уровней ряда; в) сумму уровней ряда; г) произведение уровней ряда. 6. Темп роста исчисляют: а) как отношение уровней ряда в процентах б) разность уровней ряда в процентах в) сумму уровней в процентах г) произведение уровней в процентах 7. Основная тенденция представляет собой изменение ряда динамики: а) равномерно повторяющиеся через определенные промежутки времени внутри ряда; б) определяющее общее направление развития; в) неравномерные изменения через определенные промежутки внутри года; г) через определенные промежутки времени с годичным интервалом. 8. Сезонные колебания представляют собой изменения ряда динамики: а) через определенные промежутки времени с годичным интервалом; б) внутри года; в) неравномерные изменения через определенные промежутки внутри года; г) определяющее общее направление развития. 9. Для выявления основной тенденции развития используют: а) метод укрупнения интервалов; б) метод скользящей средней; в) метод аналитического выравнивания; г) ряд Фурье. 10. Индексы сезонности можно рассчитать как отношение фактического уровня за тот или иной месяц: а) к среднемесячному уровню за год; б) выровненному уровню за тот же год; в) среднемесячному выровненному уровню за год; г) уровню ряда базисного года. 11. Ряд динамики, характеризующий уровень развития социально-экономического явления на определенные даты времени, называется: а) интервальным; b) моментным. Ряд динамики, характеризующий уровень развития социально-экономического явления за определенные отрезки времени, называется: с) интервальным; d) моментным. а) ас; б) ad; в) bc. г) bd 12. Средний уровень моментного ряда динамики исчисляется как средняя арифметическая взвешенная: а) при равных интервалах между датами; b) неравных интервалах между датами; как средняя хронологическая при: с) равных интервалах между датами; d) неравных интервалах между датами. а) ad; б) bc в) ас г) bd 13. Показатель абсолютного значения одного процента прироста равен: а) уровню ряда, деленному на темп роста; b) абсолютному приросту, деленному на темп прироста. Темп прироста исчисляется как: с) отношение уровней ряда; d) отношение абсолютного прироста к уровню ряда, взятому за базу сравнения. а) ас; б) bd в) ad г) bc 14. Для выявления основной тенденции развития используются: а) метод усреднения интервалов; b) метод скользящей средней. а) а; б) b; в) ab. г) нет ответа 15. Ряд динамики, характеризующий изменение урожайности сахарной свеклы в фермерском хозяйстве, аналитически можно представить уравнением а) 12 %; б) 12 ц; в) 230 + 12 ц. Тренировочное задание № 1 Имеются следующие данные о динамике производства тканей в одном из регионов за 2007 - 2011 гг. Рассчитать все показатели динамики по исходным данным таблицы (графы1и2). Величина абсолютного прироста (Δ y) определяется как разность двух сравниваемых уровней и вычисляется следующим образом: Δ yб = уi - у 1 - базисные показатели; Δ yц = уi - уi - 1 - цепные показатели, где уi - уровень i -го периода (кроме первого); у 1 - уровень базисного периода; уi - 1 - уровень предыдущего периода. В задании базисные показатели абсолютного прироста по сравнению с 2007 г. составит: в 2008 г. – Δ yб 08 = 267- 256 = 11 (млн м2); в 2009 г. – Δ yб 09 = 279 - 256 = 23 (млн м2) и т. д. Рассчитаем цепные показатели абсолютного прироста. Абсолютный прирост составит: в 2008 г. по сравнению с 2007 г. - Δ yц 08 = 267 - 256 = 11 (млн м2); в 2009 г. по сравнению с 2008 г. - Δ yц 09 = 279 - 267 = 12 (млн м2) и т. д. Определим темп роста (Т р), (в процентах): Тр б=( Трц= В задании базисные темпы роста составят: -в 2008 г. по сравнению с базисным 2007 г.: Тр б 08 =( - в 2009 г. по сравнению с базисным 2007 г.: Тр б 09 =( Рассчитаем цепные показатели темпа роста. - в 2008 г. по сравнению с базисным 2007 г.: Тр ц 08 =( в 2009 г. по сравнению с 2008 г.:
Тр ц 09 =( Темп прироста может быть вычислен также путем вычитания из темпов роста 100 %, т. е. Т пр = Т р – 100 %. Для примера рассчитаем темп прироста: - базисный -в 2008г. по сравнению с базисным 2007 г.: Т пр б 08 = 104, 3 - 100 = 4, 3 (%;) -в 2009 г. по сравнению с базисным 2007г.: Т пр б 09 = 109 – 100 = 9 (%) и т. д. - цепной: - в 2008г. по сравнению с базисным 2007 г.: Т пр ц 08 = 104, 3 - 100 = 4, 3 (%;) - в 2009 г. по сравнению с 2008г.:
Абсолютное значение прироста 1% составит: - в 2008 г. по сравнению с 2007г.: |%|= 0, 01 y 2007 г. = 0, 01* 256 = 2, 56 (млн м2); - в 2009 г. по сравнению с 2008 г.: |%| = 0, 01 y 2008 г. = 0, 01* 267 =2, 67 (млн м2) и т. д. Приведенная в задании таблица с вычислениями характеристик изменения уровней позволяет проводить анализ данного динамического ряда. В задании интервальный ряд динамики с равными периодами времени, поэтому средний уровень ряда рассчитается по формуле средней арифметической простой:
где n - число периодов. Средний объем производства тканей за 5 лет составил:
Средний абсолютный прирост определяется по формуле:
В задании среднегодовой прирост производства тканей за 2007-2011 гг. равен:
Среднегодовой темп роста вычисляется по формуле средней геометрической:
где n - число коэффициентов роста. Среднегодовой темп роста производства тканей за 2007- 2011 г. рассчитаем двумя способами:
Среднегодовой темп прироста равен: Т пр = 104, 5 – 100 = 4, 5 (%).
Задания для самостоятельной работы Задание 1. Имеются следующие показатели по предприятию (млн.р.):
Определите за первое полугодие: 1) среднемесячную стоимость оборотных средств за I и II кварталы и за полугодие; 2) базисные темпы роста и прироста стоимости оборотных средств; проверьте взаимосвязь между ними; 3) среднемесячный темп роста и прироста стоимости оборотных средств; 4) абсолютный прирост стоимости оборотных средств во II квартале по сравнению с I кварталом. Задание 2. Используя взаимосвязь аналитических показателей динамики, определите уровни ряда динамики производства часов производственным объединением за 2006-2011 гг. и недостающие в таблице цепные показатели динамики:
Задание 3. Имеются следующие данные о розничном товарообороте во всех каналах реализации в регионе:
Для изучения общей тенденции розничного товарооборота региона по месяцам за 2008 - 2010 гг. проведите: 1) преобразование исходных данных путем укрупнения периодов времени: а) в квартальные уровни, б) в годовые уровни; 2) сглаживание квартальных уровней розничного товарооборота с помощью скользящей средней. Изобразите графически фактические и сглаженные уровни ряда динамики. Сделайте выводы о характере тенденции розничного товарооборота по всем каналам реализации в регионе. Задание 4. Динамика выпуска реализованной продукции производственного предприятия за январь – май 2010 г. характеризуется следующими данными:
На основе этих данных за исследуемый период определите: 1) средний уровень ряда динамики; 2) среднемесячный темп роста и прироста; 3) среднемесячный абсолютный прирост. Задание 5 Используя взаимосвязь показателей динамики, определите уровни ряда динамики и недостающие в таблице базисные показатели динамики по следующим данным производства тканей в регионе за 2003-2011 г.г.
Задание 6 Произведите аналитическое выравнивание данного ряда на основе линейной функции. Имеются данные о среднем размере товарных запасов в универмагах по месяцам года млн. р.
|

 =230+12t. Это значит, что урожайность сахарной свеклы увеличивается ежегодно в среднем на:
=230+12t. Это значит, что урожайность сахарной свеклы увеличивается ежегодно в среднем на: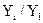 )·100 - базисные показатели;
)·100 - базисные показатели; - цепные показатели.
- цепные показатели.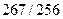 )·100 = 104, 3 (%)
)·100 = 104, 3 (%) )·100 = 109, 0 (%)
)·100 = 109, 0 (%) )·100 = 104, 5 (%)
)·100 = 104, 5 (%)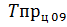 09 = 104, 5 - 100 = 4, 5 (%)
09 = 104, 5 - 100 = 4, 5 (%)
 - итог суммирования уровней за весь период;
- итог суммирования уровней за весь период;


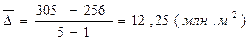

 или 104, 5 %.
или 104, 5 %. или 104, 5 %.
или 104, 5 %.


