Тема 10. Статистическое изучение взаимосвязи социально-Экономических явлений
Вопросы к изучению 1. Понятие причинности, регрессии и корреляции. 2. Парная регрессия на основе метода наименьших квадратов и метода группировок. 3. Множественная регрессия. 4. Собственно-корреляционные параметрические методы изучения связи. 5. Принятие решений на основе уравнений регрессии. 6. Методы изучения связи качественных признаков. 7. Ранговые коэффициенты связи. Тренировочное задание 1 Установить взаимосвязь чистой прибыли со стоимостным выпуском продукции по данным интервальной группировки 40 фирм, приведенным ниже (таблица 1). Таблица 1 Исходные данные
Решение тренировочного задания 1 По средним данным интервальной группировки заполняется корреляционная таблица 2. Таблица 2 Исходная таблица
Данная корреляционная таблица 2 свидетельствует о наличии прямой связи между выпуском продукции и чистой прибылью фирм, поскольку их количества расположились вокруг диагонали, идущей сверху вниз направо. Кроме того, в ней показаны средние по фирмам значения выпуска продукции и чистой прибыли. Для оценки тесноты связи рассчитывается вспомогательная таблица 3. Таблица 3 Вспомогательная таблица
Определяем линейный коэффициент корреляции по формуле
что указывает на сильную прямую связь. Для проверки значимости этого коэффициента определяется расчетное значение критерия Стьюдента по формуле:
Табличное значение критерия Стьюдента при расчетном числе степеней свободы 3 равняется 0, 137-3, 182 с вероятностью 0, 9 - 0, 05. Оно меньше расчетного значения, поэтому найденный коэффициент корреляции следует считать значимым. Далее определяем параметры линейного уравнения регрессии а0 = а1 = а0 = 31, 75 – 0, 0888* 605= - 21, 94 Следовательно, изучаемая взаимосвязь может быть выражена уравнением прямой линии в виде Ух = - 21, 94 + 0, 09 Х. Отрицательность коэффициента а0 в этом уравнении означает, что при некотором выпуске продукции балансовой прибыли может не быть, т.е. можно найти «точку безубыточности» всех рассмотренных фирм, приняв Y = 0. В этом случае получаем
При такой средней стоимости выпуска продукции фирмы будут работать без прибыли, а меньший выпуск продукции приведет к убыткам.
Тесты 1. Корреляционный анализ используется для изучения... А. взаимосвязи явлений Б. развития явления во времени В. структуры явлений
2. Определение параметров управления регрессии между двумя признаками является целью… А. выборочного метода Б. метода группировки В. корреляционного метода Г. регрессионного метода 3. Теснота связи между признаками определяется с помощью метода… А. относительных величин Б. средних величин В. корреляции Г. группировок
4. В результате проведения регрессионного анализа получают функцию, описывающую...... показателей А. взаимосвязь Б. соотношение В. структуру Г. темпы роста Д. темпы прироста
5. Прямолинейная связь между факторами исследуется с помощью уравнения регрессии..... А. Б. В. Г.
6. Для аналитического выражения нелинейной связи между факторами используются формулы....... А. Б. В.
7. Управление регрессии между двумя признаками, имеющее виду у=2, 17х0, 51, является ________ функцией. А. гиперболической Б. показательной В. степенной Г. логистической
8. Тесноту связи между двумя альтернативными качественными признаками можно измерить с помощью коэффициентов....... А. знаков Фехнера Б. корреляции рангов Спирмена В. ассоциации Г. контингенции Д. конкордации
9. Для определения степени тесноты связи между качественными признаками используется … А. коэффициент детерминации Б. коэффициент контингенции В. множественный коэффициент корреляции Г. линейный коэффициент корреляции
10. Если результативный и факторный признаки являются количественными, то для анализа тесноты связи между ними могут применяться...... А. корреляционное отношение Б. линейный коэффициент корреляции В. коэффициент ассоциации Г. коэффициент корреляции рангов Спирмена Д. коэффициент корреляции знаков Фехнера
11. Для измерения тесноты корреляционной связи между двумя количественными признаками используются....... А. коэффициент корреляции знаков Б. коэффициент эластичности В. линейный коэффициент корреляции Г. коэффициент корреляции рангов 12. Парный коэффициент корреляции показывает тесноту....... А. линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель Б. линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель В. связи между результативным признаком и остальными, включенными в модель Г. нелинейной зависимости между двумя признаками
13. Парный коэффициент корреляции может принимать значения....... А. от 0 до 1 Б. от -1 до 0 В. от -1 до 1 Г. любые положительные Д. любые меньше нуля
14. Частный коэффициент корреляции показывает тесноту....... А. линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель Б. линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель В. нелинейной зависимости Г. связи между результативным признаком и остальными, включенными в модель
15. Частный коэффициент корреляции может принимать значения....... А. от 0 до 1 Б. от -1 до 0 В. от -1 до 1 Г. любые положительные Д. любые меньше нуля
16. Множественный коэффициент корреляции может принимать значения...... А. от 0 до 1 Б. от -1 до 0 В. от -1 до 1 Г. любые положительные Д. любые меньше нуля
17. Коэффициент детерминации представляет собой долю...... А. дисперсии теоретических значений в общей дисперсии Б. межгрупповой дисперсии в общей В. межгрупповой дисперсии в остаточной Г. дисперсии теоретических значений в остаточной дисперсии
18. Коэффициент детерминации может принимать значения....... А. от 0 до 1 Б. от -1 до 0 В. от -1 до 1 Г. любые положительные Д. любые меньше нуля
19. Расчет коэффициента детерминации невозможен без значения коэффициента… А. эластичности Б. контингенции В. корреляции Г. ассоциации
20. Коэффициент эластичности потребления хлеба от дохода составляет 0, 6. Это означает что … А. потребление хлеба увеличивалось медленнее роста доходов Б. увеличение среднедушевого дохода на 10% приведет к росту потребления хлеба на 6% В. потребление хлеба уменьшилось в текущем периоде на 6% по сравнению с ростом доходов Г. прирост доходов на 1% сопровождается уменьшением потребления хлеба на 0, 4%
21. Эмпирическое корреляционное отношение представляет собой корень квадратный из отношения...... дисперсии(й). А. средней из групповых дисперсий к общей Б. межгрупповой дисперсии к общей В. межгрупповой дисперсии к средней из групповых Г. средней из групповых дисперсий к межгрупповой
22. Теснота связи двух признаков при нелинейной зависимости определяется по формуле....... А. Б.
Задания для самостоятельной работы Задание 1. На основе коэффициента корреляции рангов Спирмэна оцените тесноту связи между разрядом и среднесуточной выработкой рабочих бригады (таблица 4). Таблица 4 Исходные данные
Найдите параметры уравнения регрессии. Проанализируйте полученные результаты.
Задание 2 Взаимосвязь между ценой спроса и ценой предложения наиболее ликвидных на внебиржевом рынке акций характеризуется следующими данными (таблица 5). Таблица 5 Исходные данные
Найдите параметры уравнения регрессии. Определите направление и тесноту связи. Проанализируйте полученные результаты. Задание 3 Определите тесноту связи между урожайностью и количеством осадков на 6 участках с помощью линейного коэффициента корреляции (таблица 6). Таблица 6 Исходные данные
Найдите параметры уравнения регрессии. Проанализируйте полученные результаты. Задание 4 Зависимость сокращения рабочих от их места работы характеризуется следующими данными (таблица 7).
Таблица 7 Исходные данные
Необходимо измерить тесноту этой зависимости, если она есть. Сформулируйте выводы. Задание 5 Оцените связь между образованием рабочих цеха и наличием прогулов (таблица 8). Таблица 8 Исходные данные
Измерить тесноту этой зависимости, если она есть. Сформулируйте выводы.
|

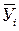
 =31, 75
=31, 75

 =605
=605




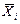

 )2
)2
 -
-  )
)
 .
.

 - а1 *
- а1 *  ; а0 = 31, 75 - а1 * 605;
; а0 = 31, 75 - а1 * 605;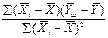 . а1 =
. а1 = 









