Решение. а) Чтобы определить равновесную цену и равновесный объем продаж, необходимо использовать условие рыночного равновесия: Qd=QS
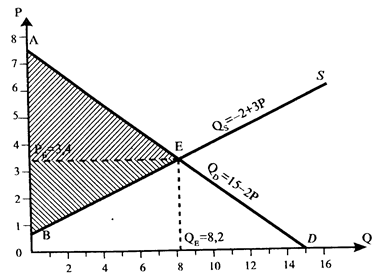
а) Чтобы определить равновесную цену и равновесный объем продаж, необходимо использовать условие рыночного равновесия: Qd=QS. В нашем примере: 15-2Р = -2+3Р, Р=3, 4. Таким образом, равновесная цена в нашем примере будет равна РE=3, 4 тыс. руб. за единицу товара. Равновесный объем продаж в нашем случае можно определить, если подставить PE в функцию спроса или функцию предложения. QE=Qd= QS= -2+ 3 х 3, 4 = 8, 2 тыс. ед. в неделю. Определить равновесные цену и объем продаж можно также графическим способом, если найти точку пересечения линий спроса и предложения из нашего примера (рис. 20.).
Рис. 20. Рассчитаем значение излишков потребителя и производителя для нашего примера. На рисунке 20 сумма излишка потребителя равна площади треугольника АРEЕ. Координаты точки А соответствуют такой цене на рынке, при которой объем спроса на товар будет ранен 0, т.е. 0=15-2Р; Р = 7, 5 тыс. руб. Значит, длина отрезка АРE = 7, 5 - 3, 4 = 4, 1. Длина отрезка РEЕ равна равновесному объему продаж, т.е. QE=8, 2. Излишек потребителя равен: S треугольникаAPEE = 1/2 х 8, 2 х 4, 1 = 16, 81. То есть, чистый выигрыш всех покупателей на рынке от приобретения товара по рыночной цене составит 16, 81 млн. руб. в неделю. Аналогичным образом рассчитаем излишек производителя. Ему соответствует площадь треугольника BPEE. Определим координаты точкиВ, то есть рассчитаем, при какой цене объем предложения товара будет равен 0. 0 = -2 + 3Р; Р = 0, 66. Длина отрезка PEB равна: PEB = 3, 4 - 0, 66 = 2, 74. Излишек производителя в нашем примере равен: S треугольника PEBE = 1/2 х 8, 2 х 2, 74 = 11, 234. Таким образом, чистый выигрыш, который получат все производители от продажи своей продукции по единой рыночной цене составит 11, 234 млн. руб. в неделю. Общественный выигрыш будет равен сумме излишков потребителя и производителя: S треугольника АЕВ = S треугольника APEE + + S треугольника BPEE = = 16, 81 + 11, 234 = = 28, 044 млн. руб. в неделю.
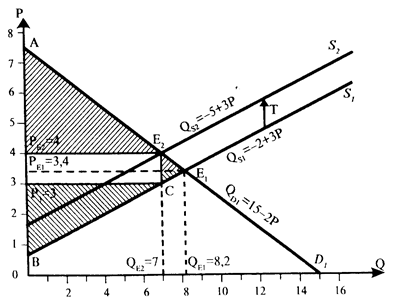
б) Допустим, что государство ввело потоварный налог в размере 1 тыс. руб. на единицу товара. В нашем случае налог будет уплачиваться в бюджет продавцом. Функция спроса Qd1=15-2Р и функция предложения QS=-2+3Р отражают первоначальную ситуацию на рынке. Так как налог уплачивает продавец, то на графике происходит сдвиг линии предложения параллельно вверх на величину Т=1 тыс. руб. (рис. 21), исходя из этого, можно вывести функцию новой линии предложения S2. Для новой функции предложения каждому предыдущему объему будет соответствовать новая цена, которая будет выше предыдущей на величину, равную ставке налога, т.е. на Т=1 тыс. руб. Следовательно, уравнение линии предложения S2 примет вид: QS=-2+3(P-1), QS = -5 + 3Р. Новые равновесные цена и объем продаж будут соответствовать координатам точки пересечения линий D1 и S2 (точка Е2). -5+3Р=15-2Р. PE2 = 4 тыс. руб. за единицу товара. QE2= 15 - 2 х 4 = 7 тыс. ед. в неделю. Цена, которую заплатят покупатели, равна PE2 = 4 тыс. руб. за ед. Цена, которую получит продавец, будет равна: P3 = PE2 -Т = 4-1=3 тыс. руб. за ед.
Рис.21. Общая сумма налога, которая поступит в бюджет государства, будет равна: QE2 х Т = 7 х 1 = 7 млн. руб. Рассчитаем, какие изменения произошли в излишках потребителя и производителя после введения правительством потоварного налога. После введения налога излишек потребителя сократился до величины, равной площади треугольника АРE2Е2 (рис. 21). S треугольника APE2E2 = 1/2 х PE2E2 х АРE2 = = 1/2 х (7, 5- 4) х 7 = 12, 5 млн. руб. в неделю. После введения налога излишек производителя сократился до величины, равной площади треугольника ВР3С (рис. 21): S треугольника ВР3С = 1 /2 х 7 х (3 - 0, 66) = 8, 19 млн. руб. в неделю. Чистый выигрыш общества после введения налога будет равен: S треугольника АРE2Е2 + S треугольника ВР3С = =12, 25 + 8, 19 = 20, 44 млн. руб. в неделю. Чистый выигрыш общества сократился на величину, равную: 28, 044 - 20, 44 = 7, 604 млн. руб. в неделю На рис. 21. эта величина равна площади фигуры РE2Е2Е1СР3. Из этой суммы, часть денег, поступившая в госбюджет от налога, равная 7 млн. руб. (площадь прямоугольника РE2Е2СР3рис. 2.) может быть использована в интересах производителей и потребителей. Чистые потери общества составят 7, 604 - 7 = 0, 604 млн. руб. в неделю. На рис. 21. чистые потери общества равны площади треугольника Е2Е1С.
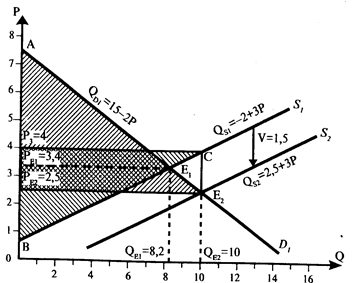
в) Рассмотрим, что произойдет с рыночным равновесием в нашем примере после установления правительством потоварной дотации (рис. 22.). Первоначальные функции спроса и предложения имели вид: Qd1=15-2Р, QS=-2+3Р.
Рис.22. Представим, что правительство начало выплачивать производителям потоварную дотацию в размере V=1, 5 тыс. руб. за ед. товара. В этом случае произойдет сдвиг линии предложения параллельно вниз на величину V=1, 5 тыс. руб. (рис. 22). Уравнение новой линии предложения S2 будет следующим: QS2 =-2+3(Р+1, 5), QS2 = 2, 5 + 3Р. Новые равновесные цена и объем: 2, 5+3Р = 15-2Р; РE2=2, 5 тыс. руб. за единицу; QE2 = 2, 5 + 3 х 2, 5 =10 тыс. ед. в неделю. РE2=2, 5 тыс. руб. за единицу – цена, которую заплатит покупатель; Р3 = РE2 + V = 2, 5+ 1, 5 = 4 тыс. руб. за единицу – цена, которую получит продавец. Общая сумма дотации из госбюджета составит: V x QE2 = 1, 5 x 10 = 15 млн. руб. в неделю. Теперь рассчитаем, как изменятся излишки потребителя и производителя после установления правительством потоварной дотации. Излишек потребителя увеличился до площади треугольника АРE2Е2 и будет равен: S треугольника АРE2Е2 =1/2 х 10 x (7, 5 - 2, 5)= 25 млн. руб. в неделю. Излишек производителя увеличился до площади треугольникаВР3С и будет равен: S треугольникаВР3С = 1/2 х 10 х (4 - 0, 66) = 16, 7 млн. руб. в неделю. Общественный выигрыш после установления дотации составит: 25 + 16, 7 = 41, 7 млн. руб. в неделю. Таким образом, общественный выигрыш увеличился на величину, равную 13, 656 млн. руб. в неделю. На рисунке 22 этой величине соответствует площадь фигуры Р3СЕ1Е2РE2. Однако денежная сумма дотации равна 15 млн. руб. в неделю (площадь прямоугольника Р3СЕ2РE2). Сумма дотации превышает величину, на которую возрос общественный выигрыш, на 15 - 13, 656 = 1, 344 млн. руб. в неделю. Эта сумма составляет чистые потери общества от установления дотации и равна по величине площади треугольника CЕ1Е2.
г) Рассмотрим, что произойдет в нашем примере, если правительство введет фиксированную цену на товар (рис. 23). Теперь представим, что государство ввело фиксированную цену на уровне ниже цены равновесия Р'=2, 5 тыс. руб. за единицу (Р'< РE1). В этом случае объем предложения будет равен: QS = -2 + 3 х 2, 5 = 5, 5 тыс. ед. в неделю. Объем спроса при этой цене составит: Qd = 15 - 2 х 2, 5 = 10 тыс. ед. в неделю. Дефицит, который возникнет на рынке, будет равен: Qd - QS = 10 - 5, 5 = 4, 5 тыс. ед. в неделю. Рис.23. В стоимостном выражении объем дефицита на рынке составит: Р' х (Qd - QS) = 2, 5 х 4, 5 = 11, 25 млн. руб. в неделю. Рассчитаем, как изменятся излишки потребителя и производителя при установлении фиксированной цены. Излишек потребителя после установления фиксированной цены будет равен площади фигуры ACDP', т.е. увеличится на площадь прямоугольника PEHDP' и сократится на площадь треугольника СНЕ (рис. 23). S прямоугольника PEHDP' = (3, 4 - 2, 5) х 5, 5 = 4, 95; S треугольника СНЕ =1/2 х НЕ х СН; НЕ = 8, 2-5, 5 = 2, 7. Чтобы определить длину отрезка СН, нужно определить координаты точки С. Координатам точки С будут соответствовать значения Р и Q функции спроса Оd = 15 - 2Р при Q = 5, 5; 5, 5 = 15-2Р; Р = 4, 75. Длина отрезка СН равна 4, 75-3, 4= 1, 35. S треугольника СНЕ = 1/2 х 2, 7 х 1, 35 = 1, 82. Значит, после установления фиксированной цены излишек потребителя будет равен: S треугольника AEPE - S треугольникаСНЕ + S прямоугольникаPEHDP' = = 16, 81 - 1, 82 + 4, 95 = 19, 94 млн. руб. в неделю. Таким образом, излишек потребителя увеличится на 19, 94 - 16, 81 = 3, 13 млн. руб. в неделю. Рассчитаем, как изменится излишек производителя после установления фиксированной цены. Величина излишка производителя в нашем примере будет равна площади треугольника P'DB: S треугольникаP'DB = 1/2 х Р'В х P'D = = 1/2 х (2, 5 -0, 66) х 2, 5 = 5, 06 млн. руб. в неделю. После введения фиксированной цены общественный выигрыш будет равен: 19, 94 + 5, 06 = 25 млн. руб. в неделю. Чистые потери общества от установления правительством фиксированной цены на уровне Р'=2, 5 тыс. руб. за единицу составят: 28, 044 - 25 = 3, 044 млн. руб. в неделю. 4-3п. Кривые спроса и предложения на товар А заданы формулами: Qd=50-6Р; Qs=4Р-10, где Р измеряется в долларах, Q – в тысячах штук. Правительство ввело акцизный налог, равный одному доллару на каждую проданную единицу товара А. а) Определите сумму налога, которую соберет налоговая служба. б) Вычислите налоговое бремя продавцов и налоговое бремя покупателей. Решение
а) 1) Найдем равновесную цену и равновесный объем продаж из уравнения QE=Qd= QS =50-6Р=4Р- 10, РЕ = 6 долл., QE =14 тыс. штук. 2) Найдем равновесную цену и равновесный объем продаж после введения акциза из уравнения 50-6Р=4(Р-1)-10; РЕ1=6, 4 долл., QE1 = 11, 6 тыс. штук. 3) Сумма налога, которую соберет налоговая служба, равна объему продаж, умноженному на ставку налога, т.е. 11, 6 х 1 = 11, 6 тыс. долл. б) Налоговое бремя покупателей равно уменьшению излишка покупателей. Решим соответствующую геометрическую задачу. До введения акциза излишек выражался площадью треугольника ( После установления налога излишек стал выражаться площадью треугольника (
Рис.24. Таким образом, налоговое бремя покупателей равно
Налоговое бремя продавцов заключается в уменьшении их излишка, выражающегося площадью трапеции 6; 5, 4; А, Е. Эта площадь равна полусумме Итого налоговое бремя продавцов: (11, 6 + 14) х Ответ: а) 11, 6 тыс. долл. б) Налоговое бремя покупателей равно 5, 12 тыс. долл. Налоговое бремя на продавцов составит 7, 68 тыс. долл.
|


 , 6, Е), т.е. равнялся 14 х (
, 6, Е), т.е. равнялся 14 х ( тыс. долл.
тыс. долл. -6, 4)/2 тыс. долл. = 11, 213 тыс. долл.
-6, 4)/2 тыс. долл. = 11, 213 тыс. долл.
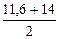 умноженной на высоту (6-5, 4).
умноженной на высоту (6-5, 4). = 7, 68 тыс. долл.
= 7, 68 тыс. долл.


