Отделение корней уравнения
Пусть дано уравнение, которое в общем виде записывается формулой
где f(x) любая действительная функция. Точным корнем уравнения (2.1) на конечном или бесконечном отрезке [ α, β ] назовем всякое число ξ из промежутка, которое обращает функцию.f(x) в нуль. Так как уравнение может быть достаточно сложным, редко удается найти его точные корни. Задача состоит в том, чтобы найти приближенные корни и оценить, насколько точно это сделано. Процесс нахождения приближенных корней уравнения общего вида f(x) = 0 проводится в два этапа: 1. Отделение корней, то есть установление возможно малых промежутков 2. Уточнение приближенных корней. Если ξ -точный корень, x приближенный корень уравнения (2.1), а ε точность, то для того, чтобы приближенный корень x был найден с заданной точностью ε достаточно потребовать выполнения неравенства: Теорема 2.1: Если непрерывная функция Корень
|
, (2.1)
, в которых содержится один и только один корень уравнения (2.1);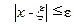
.
принимает значения противоположных знаков на концах 
, то внутри этого отрезка содержится, по меньшей мере, один корень уравнения 
.
[ 
] заведомо будет единственным, если производная 
существует и сохраняет постоянный знак внутри интервала 
, т.е. 
(или 
) при 
.
