Интерполяционный многочлен Лагранжа
Для произвольно заданных узлов интерполирования пользуются более общей формулой, так называемой интерполяционной формулой Лагранжа. Пусть на отрезке Решим сначала частную задачу, построив полином такой, что Т.к. искомый полином обращается в нуль в n точках
где
Отсюда Вернемся к выражению (5.1):
Тогда полином Лагранжа имеет следующий вид:
Докажем единственность полинома Лагранжа. Предположим противное. Пусть При равноотстоящих точках таблицы xi многочлен Лагранжа совпадает с многочленом Ньютона такой же степени.
|

 даны n+1 различных значений аргумента:
даны n+1 различных значений аргумента:  , и известны значения для функции
, и известны значения для функции 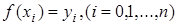 . Нам нужно построить многочлен
. Нам нужно построить многочлен  .
. .
. , то он имеет вид:
, то он имеет вид: , (5.1)
, (5.1) - постоянный коэффициент. Полагая
- постоянный коэффициент. Полагая  в формуле и учитывая, что
в формуле и учитывая, что  , получим:
, получим: .
.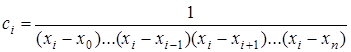 .
. .
.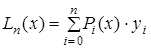 .
. - полином, отличный от
- полином, отличный от  , степень его не выше n и
, степень его не выше n и 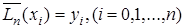 . Тогда полином
. Тогда полином  , степень которого, очевидно, не выше n, обращается в нуль в n+1 точках
, степень которого, очевидно, не выше n, обращается в нуль в n+1 точках  . Следовательно,
. Следовательно, 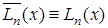 .
.


