Вычисление лагранжевых коэффициентов
Можно записать лагранжевы коэффициенты и более компактно: где Формула Лагранжа при этом имеет вид Для вычисления лагранжевых коэффициентов может быть использована приведенная ниже схема. Сначала располагаем в таблицу разности
Таблица 5.3. Таблица разностей
Обозначим произведение элементов первой строки через D0, второй – D1 и т.д. Произведение же элементов главной диагонали, очевидно, будет
Пример 5.3 Выполнено в Mathcad Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лангранжа, если функция задана в неравно- отстоящих узлах таблицы.
Рис 5.2. Решения примера 5.3 в Mathcad
Отметим, что форма лагранжевых коэффициентов инвариантна относительно целой линейной подстановки
после подстановки и сокращения числителя и знаменателя на an, получим:
или
где В случае равноотстоящих точек лагранжевы коэффициенты могут быть приведены к более простому виду. В самом деле, полагая
Тогда где
где
Пример 5.4 Выполно в Mathcad. Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лагранжа, если функция задана в равноотстоящих узлах таблицы
Рис 5.3. Решения примера 5.4 в Mathcad
|
(5.2)
, (5.3)
.
.
. Отсюда следует, что
.Следовательно,
.
(a, b – постоянны). Действительно, положив в формуле (5.2):
, 
, 
,
,
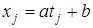, что и требовалось доказать.
, будем иметь: 
. Отсюда
и
.
,
. Отсюда можно записать:
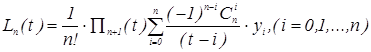(5.4)
